Arrange Given Numbers to Form Biggest Number

Problem Statement

Given an array of numbers, arrange the numbers in such a way that the number formed from their concatenation will be of the largest possible value.

Sample Test Cases:

Input 1:

s = [546, 54, 548, 60]

Output 1:

6054854654

Explanation 1:

Among all the permutations of the array, the order [60, 548, 546, 54] gives the largest concatenated number possible.

Input 2:

s = [1, 34, 3, 98, 9, 76, 45, 4]

Output 2:

998764543431

Explanation 2:

Among all the permutations of the array, the order [9, 98, 76, 45, 4, 34, 3, 1] gives the largest concatenated number possible.

Approach

The idea is to sort the numbers in descending order, and then just concatenate them. However, observe that just sorting in descending order won’t give us our optimal answer.

Take the example of 431 and 50, our code will concatenate it in order 43150 but observe that 50431 gives us a better result. So, the idea comes that we need to implement a custom sorting algorithm that sorts our array in a manner that we can obtain our optimal answer by concatenating it.

How to Sort the Array?

To compare the numbers A and B, we can view both of them as strings, and make them of the same length by calculating (A + B) and (B + A). Then we can just compare these 2 strings lexicographically, and sort them according to it.

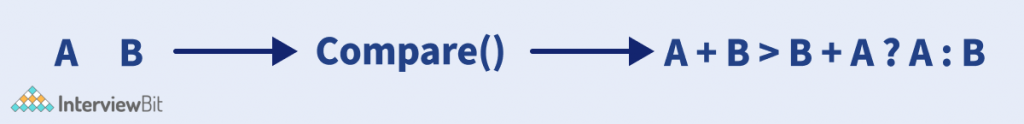
Code / Implementation:

C++ Code

string largestNumber(vector < string > & a) {
  sort(a.begin(), a.end(), [ & ](const string & x,
    const string & y) {
    string newX = x + y;
    string newY = y + x;
    return newY < newX;
  });
  string ans = "";
  for (auto x: a) {
    ans += x;
  }
  return ans;
}

Java Code

public static String largestNumber(Vector < String > a) {
  Collections.sort(a, new Comparator < String > () {
    public int compare(String first, String second) {
      String newF = first + second;
      String newS = second + first;
      return newF.compareTo(newS) <= 0 ? 1 : -1;
    }
  });
  String ans = "";
  Iterator itr = a.iterator();
  while (itr.hasNext()) {
    ans += itr.next();
  }
  return ans;
}

Python Code

from functools import cmp_to_key


def largestNumber(s):
    s = map(str, s)
    key = cmp_to_key(lambda a, b: 1 if a + b >= b + a else -1)
    res = "".join(sorted(s, key=key, reverse=True))
    res = res.lstrip("0")
    return res if res else "0"

Complexity Analysis:

• Time Complexity: O(n * log(n))
• Space Complexity: O(1)

Practice Problem:

Largest Number

FAQs

1. How can the implementation of this problem be made easier?

A. The implementation of this problem becomes easier when we work with the numbers as strings.

2. What is the custom sorting method used in this problem called?

A. Such custom sorting methods are usually called Comparators.