Construct Tree from Inorder and Preorder

Given two arrays inorder[] and preorder[], which represents the inorder and the preorder traversal of a binary tree. The task is to construct the tree from the given order and return it.

Examples:Input:
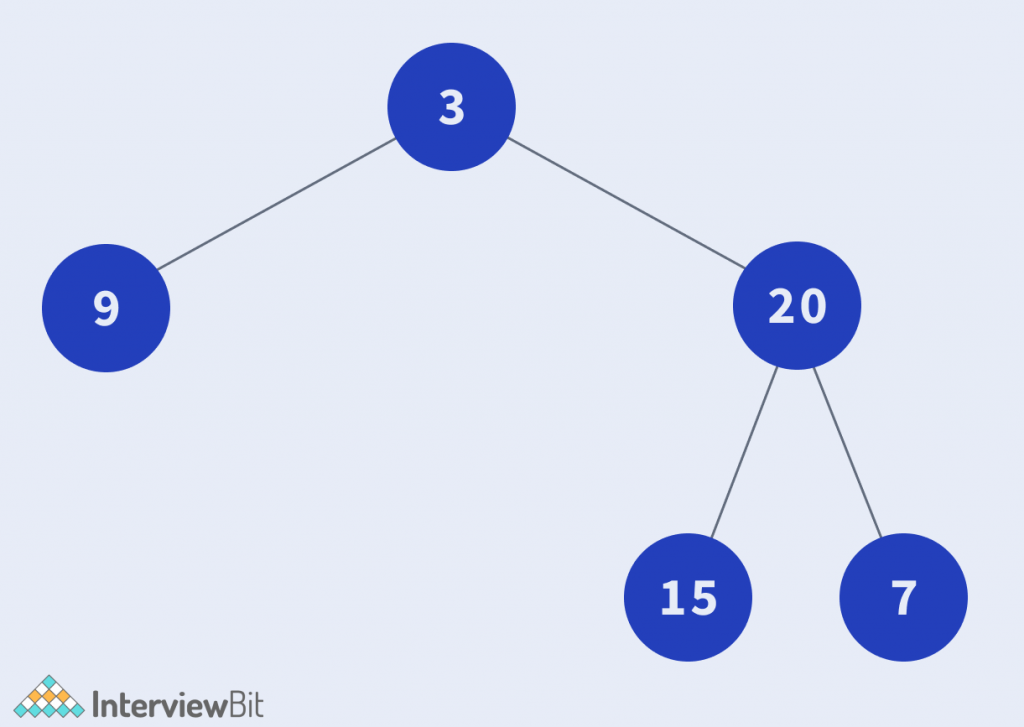
preorder[] = {3,9,20,15,7}
inorder[] = {9,3,15,20,7}
                                     
Output: {3,9,20,null,null,15,7}
Explanation: 

Approach: Recursion

We already know that in Preorder traversal, we traverse from ROOT  -> LEFT -> RIGHT. Therefore, we can easily determine the root of the resultant tree which is preorder[0].

Similarly, if you remember Inorder traversal, we traverse from LEFT -> ROOT -> RIGHT. So, if we can find the position of the Root in the inorder[], we can recursively divide the left and the right subtrees.

Follow the below method:

Algorithm:

• Initialise a hashmap to find the index of the root.
• Maintain a variable which contains all the keys and value to be used in the final binary tree.
• Construct a recursive function, which takes the inorder array as an argument and for each iteration, recursively built the left and right subtree by comparing the values with the position of the root.

Implementation of the Approach:

C++ Code

struct Node * buildTree(char in [], char pre[], int inStrt,
  int inEnd, unordered_map < char, int > & mp) {
  static int preIndex = 0;
 
  if (inStrt > inEnd)
    return NULL;
 
  char curr = pre[preIndex++];
  struct Node * tNode = newNode(curr);
 
  if (inStrt == inEnd)
    return tNode;
 
  int inIndex = mp[curr];
 
  tNode -> left = buildTree( in , pre, inStrt, inIndex - 1, mp);
  tNode -> right = buildTree( in , pre, inIndex + 1, inEnd, mp);
 
  return tNode;
}
 
struct Node * buldTreeWrap(char in [], char pre[], int len) {
  unordered_map < char, int > mp;
  for (int i = 0; i < len; i++)
    mp[ in [i]] = i;
 
  return buildTree( in , pre, 0, len - 1, mp);
}
void printInorder(struct Node * node) {
  if (node == NULL)
    return;
  printInorder(node -> left);
  printf("%c ", node -> data);
  printInorder(node -> right);
}

Java Code

 class Tree {
 
  public static Node root;
  static HashMap < Character, Integer > mp = new HashMap < > ();
  static int preIndex = 0;
 
  public static Node buildTree(char[] in , char[] pre, int inStrt, int inEnd) {
 
    if (inStrt > inEnd) {
      return null;
    }
    char curr = pre[preIndex++];
    Node tNode;
    tNode = new Node(curr);
    if (inStrt == inEnd) {
      return tNode;
    }
    tNode.left = buildTree( in , pre, inStrt, inIndex - 1);
    tNode.right = buildTree( in , pre, inIndex + 1, inEnd);
    return tNode;
  }
  public static Node buldTreeWrap(char[] in , char[] pre, int len) {
    for (int i = 0; i < len; i++) {
      mp.put( in [i], i);
    }
    return buildTree( in , pre, 0, len - 1);
  }
  static void printInorder(Node node) {
    if (node == null) {
      return;
    }
    printInorder(node.left);
    System.out.print(node.data + " ");
    printInorder(node.right);
  }

Python Code

def buildTree(inn, pre, inStrt, inEnd):
 
    global preIndex, mp
 
    if inStrt > inEnd:
        return None
 
    curr = pre[preIndex]
    preIndex += 1
    tNode = Node(curr)
 
    if inStrt == inEnd:
        return tNode
 
    inIndex = mp[curr]
 
    tNode.left = buildTree(inn, pre, inStrt, inIndex - 1)
    tNode.right = buildTree(inn, pre, inIndex + 1, inEnd)
 
    return tNode
 
 
def buldTreeWrap(inn, pre, lenn):
 
    global mp
 
    for i in range(lenn):
        mp[inn[i]] = i
 
    return buildTree(inn, pre, 0, lenn - 1)
 
 
def prInorder(node):
 
    if node == None:
        return
 
    prInorder(node.left)
    print(node.data, end=" ")
    prInorder(node.right)

Time Complexity: O(N), where N is the size of the two arrays

Space Complexity: O(N), as hashmap is used.

Practice Questions:

Construct Binary Tree From Inorder And Preorder

FAQ

• What are preorder, inorder and postorder traversals?
  These are three types of DFS traversals:
  1. Preorder – Traverses from ROOT -> LEFT -> RIGHT
  2. Inorder – Traverses from LEFT -> ROOT -> RIGHT
  3. Postorder – Traverses from LEFT -> RIGHT -> ROOT