Tree Diameter – Diameter of a Binary Tree

Problem Statement

Given a binary tree, find the diameter of the tree.

Diameter: The diameter of a tree is the length of the longest path between any 2 nodes of a tree. The length of a path is counted as the number of edges lying on that path.

Sample Test Cases

Input 1:

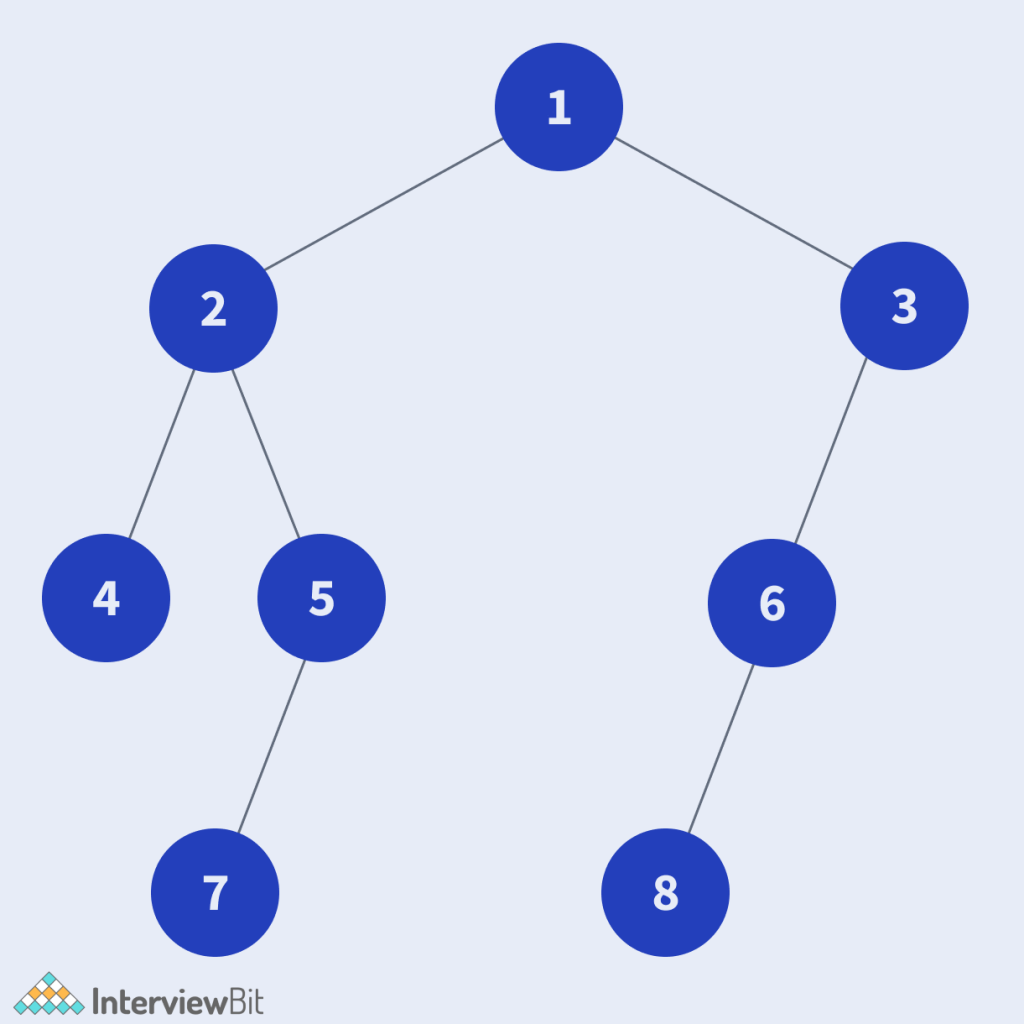
Output 1: 6
Explanation 1: The path of the tree which is the diameter is [7, 5, 2, 1, 3, 6, 8].

Input 2:

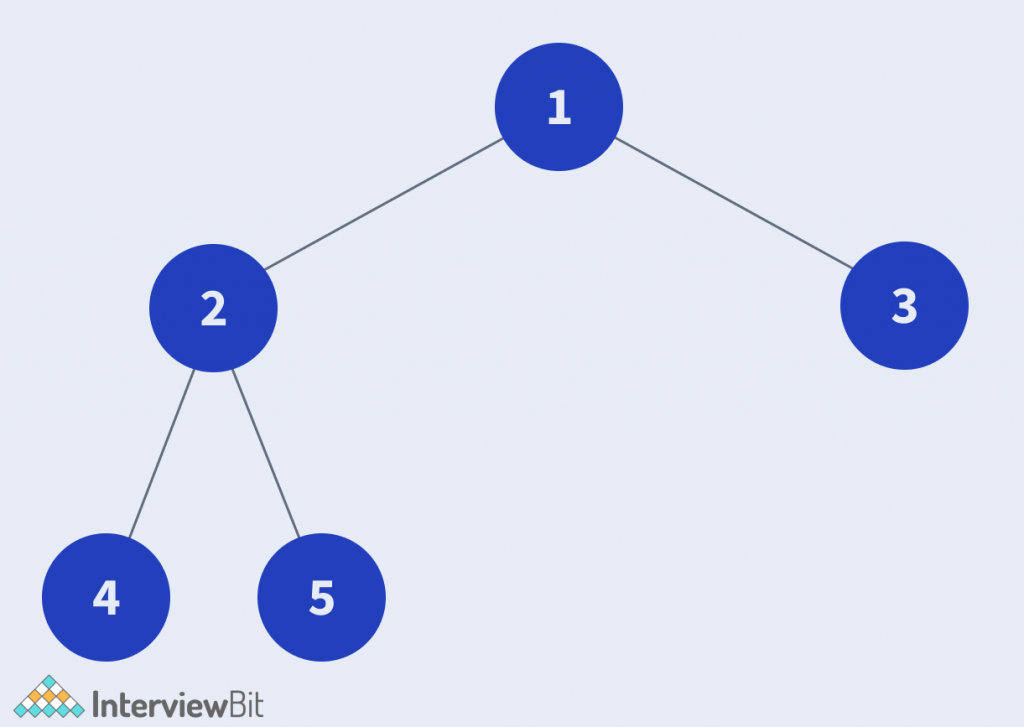
Output 2: 3
Explanation 2: The diameter path of the tree is [4, 2, 1, 3] or [5, 2, 1, 3].

Naive Approach

We note that the diameter of a tree can be written as the maximum of the diameter of the left subtree of the current node, the diameter of the right subtree of the current node, and the diameter of the current tree. We can recursively calculate the sum of the left and right subtree to get the diameter of the current tree and update the maximum value of diameter by the sum for each node in a recursive manner using DFS.

C++ Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getDepth(TreeNode *root) {
        if(root == NULL) {
            return 0;
        }
        int leftSubtreeDepth = getDepth(root->left);
        int rightSubtreeDepth = getDepth(root->right);
        return max(leftSubtreeDepth, rightSubtreeDepth) + 1;
    }
    int diameterOfBinaryTree(TreeNode* root) {
        if(root == NULL) {
            return 0;
        }
        int leftSubtreeDiameter = diameterOfBinaryTree(root->left);
        int rightSubtreeDiameter = diameterOfBinaryTree(root->right);
        int diameter = getDepth(root->left) + getDepth(root->right);
        diameter = max(diameter, max(leftSubtreeDiameter, rightSubtreeDiameter));
        return diameter;
    }
};

Java Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int getDepth(TreeNode root) {
		if(root == null) {
			return 0;
		}
		int leftSubtreeDepth = getDepth(root.left);
		int rightSubtreeDepth = getDepth(root.right);
		return Math.max(leftSubtreeDepth, rightSubtreeDepth) + 1;
	}
    public int diameterOfBinaryTree(TreeNode root) {
        if(root == null) {
			return 0;
		}
		int leftSubtreeDiameter = diameterOfBinaryTree(root.left);
		int rightSubtreeDiameter = diameterOfBinaryTree(root.right);
		int diameter = getDepth(root.left) + getDepth(root.right);
		diameter = Math.max(diameter, Math.max(leftSubtreeDiameter, rightSubtreeDiameter));
		return diameter;
    }
}

Python Code

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def getDepth(self, root):
        if not root:
            return 0
        leftSubtreeDepth = self.getDepth(root.left)
        rightSubtreeDepth = self.getDepth(root.right)
        return max(leftSubtreeDepth, rightSubtreeDepth) + 1
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0;
        leftSubtreeDiameter = self.diameterOfBinaryTree(root.left);
        rightSubtreeDiameter = self.diameterOfBinaryTree(root.right);
        diameter = self.getDepth(root.left) + self.getDepth(root.right);
        diameter = max(diameter, max(leftSubtreeDiameter, rightSubtreeDiameter));
        return diameter;

Time Complexity: O(n^2)
Space Complexity: O(1) // If recursion stack space is ignored

Optimal Approach

The idea for the optimal approach is the same as that for the naive approach. However, in the optimal approach, we change the implementation such that the calculation for depths of the subtrees and the maximum diameter of the tree, is done in the same recursive function simultaneously to optimize the time complexity.

C++ Implementation

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getMaxDepth(TreeNode* root, int &diameter) {
        if(root == NULL) {
            return 0;
        }
        int leftSubtreeDepth = getMaxDepth(root->left, diameter);
        int rightSubtreeDepth = getMaxDepth(root->right, diameter);
        diameter = max(diameter, leftSubtreeDepth + rightSubtreeDepth);
        return max(leftSubtreeDepth, rightSubtreeDepth) + 1;
    }
    int diameterOfBinaryTree(TreeNode* root) {
        int diameter = 0;
        getMaxDepth(root, diameter);
        return diameter;
    }
};

Java Implementation

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    static int diameter;
	int getMaxDepth(TreeNode root) {
		if(root == null) {
			return 0;
		}
		int leftSubtreeDepth = getMaxDepth(root.left);
		int rightSubtreeDepth = getMaxDepth(root.right);
		diameter = Math.max(diameter, leftSubtreeDepth + rightSubtreeDepth);
		return Math.max(leftSubtreeDepth, rightSubtreeDepth) + 1;
	}
    public int diameterOfBinaryTree(TreeNode root) {
        diameter = 0;
		getMaxDepth(root);
		return diameter;
    }
}

Python Implementation

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    diameter = 0
    def getMaxDepth(self, root):
        if not root:
            return 0
        leftSubtreeDepth = self.getMaxDepth(root.left)
        rightSubtreeDepth = self.getMaxDepth(root.right)
        self.diameter = max(self.diameter, leftSubtreeDepth + rightSubtreeDepth)
        return max(rightSubtreeDepth, leftSubtreeDepth) + 1
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        self.diameter = 0
        self.getMaxDepth(root)
        return self.diameter

Time Complexity: O(N)
Space Complexity: O(1) // If recursion stack space is ignored.

Practice Problem – Largest Distance Between Nodes of a Tree

Additional Resources

• Binary Tree
• Top view of Binary Tree
• Level Order Traversal of Binary Tree
• Bottom View of Binary Tree
• Inorder Traversal of a Binary Tree
• Left View of a Binary Tree