Problem Statement
Graph colouring problem involves assigning colours to certain elements of a graph subject to certain restrictions and constraints. In other words, the process of assigning colours to the vertices such that no two adjacent vertexes have the same colour is called Graph Colouring.
This is also known as vertex colouring.
Example:
Confused about your next job?
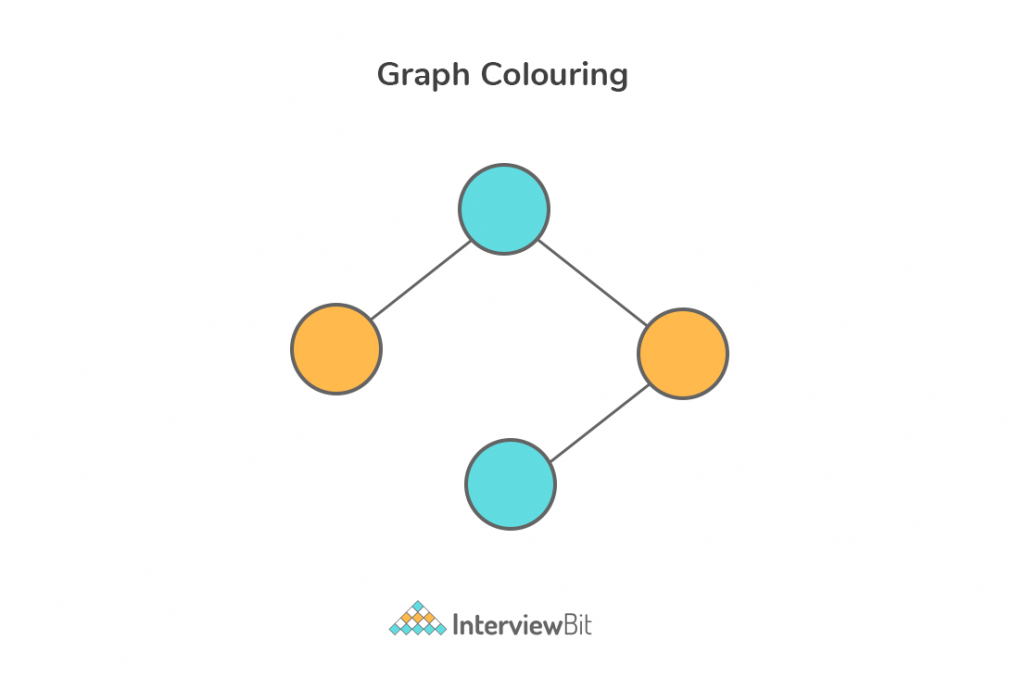
Chromatic Number: The smallest number of colours needed to colour a graph G is called its chromatic number.
For example, in the above image, vertices can be coloured using a minimum of 2 colours.
Hence the chromatic number of the graph is 2.
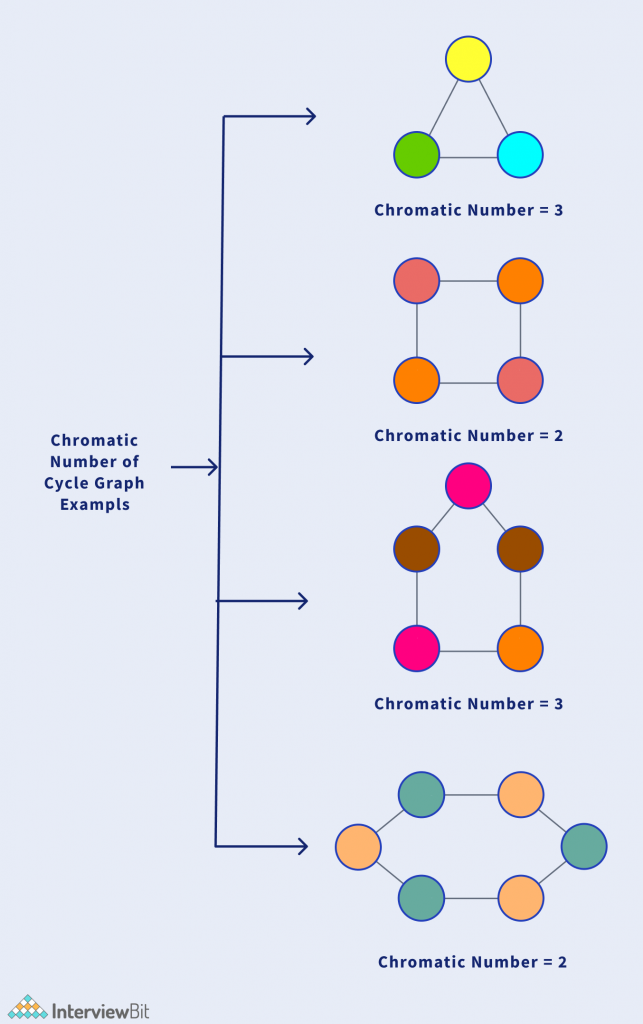
Further examples for a more clear understanding:
Applications of Graph Colouring:
- Map Coloring
- Scheduling the tasks
- Preparing Time Table
- Assignment
- Conflict Resolution
- Sudoku
Approach 1: Brute Force
- The simplest approach to solve this problem would be to generate all possible combinations (or configurations) of colours.
- After generating a configuration, check if the adjacent vertices have the same colour or not. If the conditions are met, add the combination to the result and break the loop.
- Since each node can be coloured by using any of the M colours, the total number of possible colour configurations are mV. The complexity is exponential which is very huge.
C++ Implementation
bool isSafeToColor(vector < vector < int >> & graph, vector < int > color) {
for (int i = 0; i < V; i++)
for (int j = i + 1; j < V; j++)
if (graph[i][j] == 1 && color[j] == color[i])
return false;
return true;
}
void printColorArray(vector < int > color) {
cout << ("Solution colors are: ") << endl;
for (int i = 0; i < color.size(); i++) {
cout << (color[i]);
}
}
bool graphColoring(vector < vector < int >> & graph, int m, int i, vector < int > color) {
if (i == V) {
if (isSafeToColor(graph, color)) {
printColorArray(color);
return true;
}
return false;
}
for (int j = 1; j <= m; j++) {
color[i] = j;
if (graphColoring(graph, m, i + 1, color))
return true;
color[i] = 0;
}
return false;
}Java Implementation
private static boolean isSafeToColor(int[][] graph, int[] color) {
for (int i = 0; i < V; i++)
for (int j = i + 1; j < V; j++)
if (graph[i][j] == 1 && color[j] == color[i])
return false;
return true;
}
private static void printColorArray(int[] color) {
System.out.println("Solution colors are: ")
for (int i = 0; i < color.length; i++) {
System.out.println(color[i]);
}
}
private static boolean graphColoring(int[][] graph, int m, int i, int[] color) {
if (i == V) {
if (isSafeToColor(graph, color)) {
printColorArray(color);
return true;
}
return false;
}
for (int j = 1; j <= m; j++) {
color[i] = j;
if (graphColoring(graph, m, i + 1, color))
return true;
color[i] = 0;
}
return false;
}Python Implementation
def isSafeToColor(graph, color):
for i in range(V):
for j in range(i + 1, V):
if graph[i][j] == 1 and color[j] == color[i]:
return False
return True
def printColorArray(color):
print("Solution colors are: ")
for i in range(len(color)):
print(color[i], end=" ")
def graphColoring(graph, m, i, color):
if i == V:
if isSafeToColor(graph, color):
printColorArray(color)
return True
return False
for j in range(1, m + 1):
color[i] = j
if graphColoring(graph, m, i + 1, color):
return True
color[i] = 0
return false- Time Complexity: O(M^V), where M is the total colours needed and V is the total vertices
- Space Complexity: O(V), as extra space is used for colouring vertices.
Approach 2: Backtracking
In the previous approach, trying and checking every possible combination was tedious and had an exponential time complexity.
Some of the permutation calculations were unnecessary but were calculated again and again. Therefore, the idea is to use a backtracking approach to solve the problem.
In this approach, the idea is to color a vertex and while coloring any adjacent vertex, choose a different color. Similarly, color every possible vertex following the restrictions, till any further vertex is left coloring. In any case, if all adjacent vertices for a given vertex are colored, then backtrack and change color.
If after coloring, if we return back to the same vertex that was started with and all colors are used, then more colors are needed. Hence, return False.
Algorithm
- Consider a color and check if it is valid i.e. from the given vertex check whether its adjacent vertices have been coloured with the same color.
- If true, pick a different colour, else continue colouring the vertices.
- If no other color is left un-used, then backtrack.
C++ Code
class InterviewBit {
public:
int V = 4;
bool isSafeToColor(int v, vector < vector < int >> & graphMatrix, vector < int > color, int c) {
for (int i = 0; i < V; i++)
if (graphMatrix[v][i] == 1 && c == color[i])
return false;
return true;
}
bool graphColorUtil(vector < vector < int >> & graphMatrix, int m, vector < int > color, int v) {
if (v == V)
return true;
for (int i = 1; i <= m; i++) {
if (isSafeToColor(v, graphMatrix, color, i)) {
color[v] = i;
if (graphColorUtil(graphMatrix, m, color, v + 1))
return true;
color[v] = 0;
}
}
return false;
}
void printColoringSolution(int color[]) {
cout << ("Color schema for vertices are: ") << endl;
for (int i = 0; i < V; i++)
cout << (color[i]) << endl;
}
bool graphColoring(vector < vector < int >> & graphMatrix, int m) {
vector < int > color(V, 0);
if (!graphColorUtil(graphMatrix, m, color, 0)) {
cout << "Color schema not possible" << endl;
return false;
}
printColoringSolution(color);
return true;
}Java Code
public class InterviewBit {
final int V = 4;
int[] color;
boolean isSafeToColor(int v, int[][] graphMatrix, int[] color, int c)
{
for (int i = 0; i < V; i++)
if (graphMatrix[v][i] == 1 && c == color[i])
return false;
return true;
}
boolean graphColorUtil(int[][] graphMatrix, int m, int[] color, int v)
{
if (v == V)
return true;
for (int i = 1;i <= m; i++)
{
if (isSafeToColor(v, graphMatrix, color, i))
{
color[v] =i;
if (graphColorUtil(graphMatrix, m, color, v + 1))
return true;
color[v] = 0;
}
}
return false;
}
void printColoringSolution(int color[])
{
System.out.println("Color schema for vertices are: ");
for (int i = 0; i < V; i++)
System.out.println(color[i]);
}
boolean graphColoring(int[][] graphMatrix, int m)
{
color = new int[V];
Arrays.fill(color,0);
if (!graphColorUtil(graphMatrix, m, color, 0))
{
System.out.println(
"Color schema not possible");
return false;
}
printColoringSolution(color);
return true;
}Python Code
class InterviewBit:
V = 4;
def isSafeToColor(v, graphMatrix, color, c):
for i in range(V):
if graphMatrix[v][i] == 1 and c == color[i]:
return False;
return True;
def graphColorUtil(graphMatrix, m, color, v):
if v == V:
return True;
for i in range(1, m + 1):
if isSafeToColor(v, graphMatrix, color, i):
color[v] =i;
if graphColorUtil(graphMatrix, m, color, v + 1):
return True;
color[v] = 0;
return false;
def printColoringSolution(color):
print("Color schema for vertices are: ")
for i in range(V):
print(color[i])
def graphColoring(graphMatrix, m):
color = [0]*(V)
if !graphColorUtil(graphMatrix, m, color, 0):
print("Color schema not possible")
return False;
printColoringSolution(color);
return True;- Time Complexity: O(M^V), in the worst case.
- Space Complexity: O(V), as extra space is used for colouring vertices.
Frequently Asked Questions (FAQs)
Q.1: What is the Chromatic Number
Ans: The smallest number of colours needed to colour a graph G is called its chromatic number.
Q.2: What does the backtracking approach have the same time complexity as the brute force approach?
Ans: The backtracking approach is also a type of brute force. It is just used to eliminate bad decisions while colouring the vertices.







 Join WhatsApp Group
Join WhatsApp Group