Happy Number

Problem Statement

Given an integer N. The task is to determine if N is a Happy Number.

A  Happy number is a number defined by the following process:

• Start with any positive integer, and replace the number with the sum of the squares of its digits.
• Repeat the process until the number equals 1, or it loops endlessly in a cycle which does not include 1.
• Those numbers for which this process ends in 1 are happy numbers.

Examples:

• Input: N = 97
• Output: True

Explanation:

Input:  N = 2
Output: False

Approach 1: Cycle Detection using HashSet

Let us understand this approach with an example.

Let us dry run the following:

• N = 7
• Squaring, N = 49. Now, N = 4^2 + 9 ^ 2 = 97. 
• N = 9^2 + 7^2 = 130
• N = 1^2 + 3^2 + 0^2 = 10
• N = 1^0 + 0^2 = 1

So, N becomes 1, hence, 7 is a happy number.

Let us take another example, where the number remains in a loop.

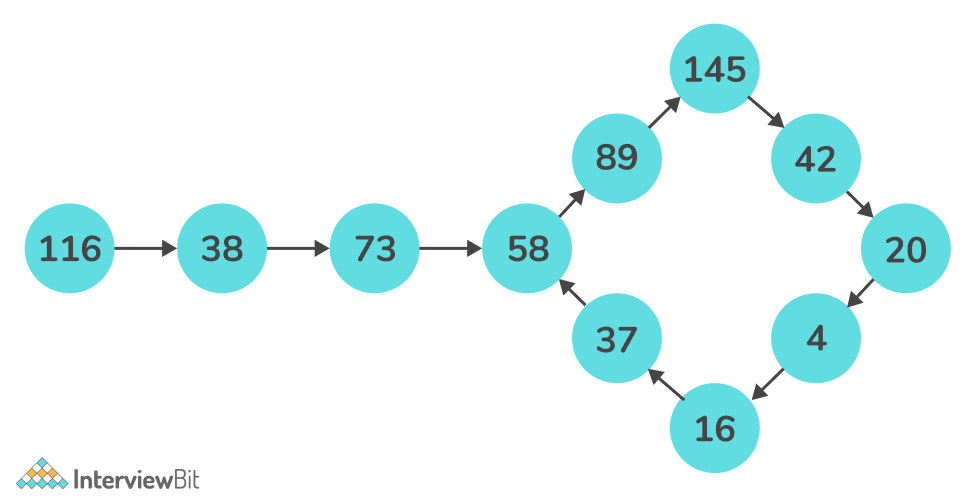
In the above example, it can be clearly observed that, after a few steps, the loops remains in a loop and can never reach 1, hence 116 is not a happy number.

Algorithm:

• Initialise a hashset to determine whether an integer has occurred previously or not.
• Initialise an integer with N and the next integer generated would be the sum of squares of digits of the current integer.
• Repeat the above process, until N reaches 1 or a number which has previously occurred again appears, i.e. enters into a cycle.
• Return True if N reaches 1, else return False.

C++Code

int getNext(int n) {
        int totalSum = 0;
        while (n > 0) {
            int d = n % 10;
            n = n / 10;
            totalSum += d * d;
        }
        return totalSum;
    }
 
    bool isHappy(int n) {
        set<int> seen;
        while (n != 1 && seen.find(n) == seen.end()) {
            seen.insert(n);
            n = getNext(n);
        }
        return n == 1;
    }

JavaCode

private int getNext(int n) {
        int totalSum = 0;
        while (n > 0) {
            int d = n % 10;
            n = n / 10;
            totalSum += d * d;
        }
        return totalSum;
    }
 
    public boolean isHappy(int n) {
        Set<Integer> seen = new HashSet<>();
        while (n != 1 && !seen.contains(n)) {
            seen.add(n);
            n = getNext(n);
        }
        return n == 1;
    }

PythonCode

def get_next(n):
        total_sum = 0
        while n > 0:
            n, digit = divmod(n, 10)
            total_sum += digit ** 2
        return total_sum
 
    seen = set()
    while n != 1 and n not in seen:
        seen.add(n)
        n = get_next(n)
 
    return n == 1

Time Complexity: O(logN)
Space Complexity: O(N), since HashSet is used.

Approach 2: Floyd’s Cycle Detection Algorithm

If an integer is not a Happy number, after certain steps it gets into the cycle. Now, this cycle can be thought of as a linked list and then our task would be to simply detect if a cycle exists in a linked list.

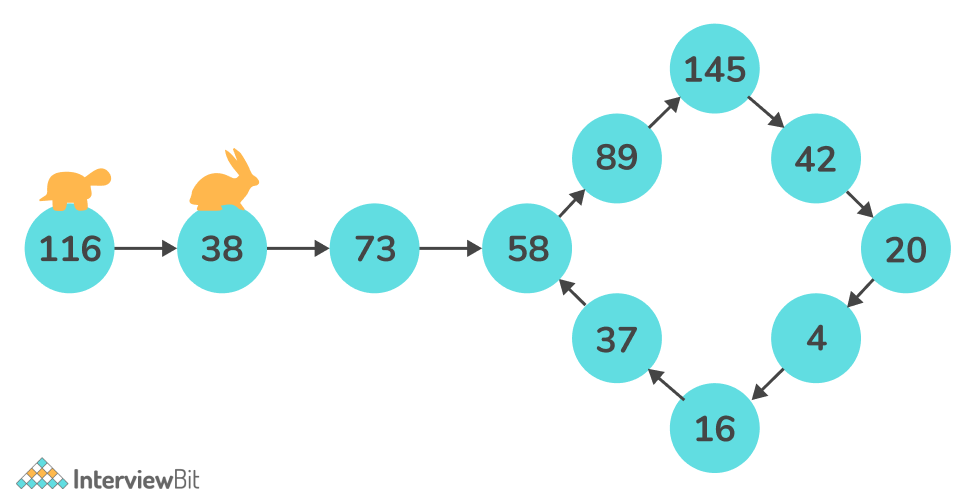
Floyd’s Cycle Detection Algorithm is based on two-pointers- fast and slow pointers. The slow pointer moves ahead by one step at a time, whereas the fast pointer moves ahead by two steps at a time. In case, there is a cycle, both the fast and slow pointer eventually meet after at a certain point.

Algorithm:

• Initialise slow pointer with N and fast pointer with the sum of squares of digits of N.
• While fast pointer doesn’t become equal to 1 and slow and fast pointer doesn’t meet,
  • Replace slow with the sum of squares of digits of slow.
  • Replace fast with the sum of squares of digits of fast.
• Return True if fast becomes 1, else return False.

C++Implementation

int getNext(int n) {
        int totalSum = 0;
        while (n > 0) {
            int d = n % 10;
            n = n / 10;
            totalSum += d * d;
        }
        return totalSum;
    }
 
    bool isHappy(int n) {
        int slowRunner = n;
        int fastRunner = getNext(n);
        while (fastRunner != 1 && slowRunner != fastRunner) {
            slowRunner = getNext(slowRunner);
            fastRunner = getNext(getNext(fastRunner));
        }
        return fastRunner == 1;
    }
}

JavaImplementation

public int getNext(int n) {
        int totalSum = 0;
        while (n > 0) {
            int d = n % 10;
            n = n / 10;
            totalSum += d * d;
        }
        return totalSum;
    }
 
    public boolean isHappy(int n) {
        int slowRunner = n;
        int fastRunner = getNext(n);
        while (fastRunner != 1 && slowRunner != fastRunner) {
            slowRunner = getNext(slowRunner);
            fastRunner = getNext(getNext(fastRunner));
        }
        return fastRunner == 1;
    }
}

PythonImplementation

def get_next(number):
        total_sum = 0
        while number > 0:
            number, digit = divmod(number, 10)
            total_sum += digit ** 2
        return total_sum
 
    slow_runner = n
    fast_runner = get_next(n)
    while fast_runner != 1 and slow_runner != fast_runner:
        slow_runner = get_next(slow_runner)
        fast_runner = get_next(get_next(fast_runner))
    return fast_runner == 1

• Time Complexity: O(logN)
• Space Complexity: O(1)

Practice Question

• N digit numbers with digit sum S

FAQ

Q.1: How do you handle the case, if the integer goes on increasing till infinity?

Ans: You do not need to explicitly handle this case, since any number until a 32-bit integer would remain in a cycle of 1053(The sum of squares of digits of 9999999999999 is 1053).

Q.2: What is Floyd’s cycle detection algorithm?

Ans: Floyd’s Cycle Detection Algorithm is based on two-pointers- fast and slow pointers. The slow pointer moves ahead by one step at a time, whereas the fast pointer moves ahead by two steps at a time. In case, there is a cycle, both the fast and slow pointers eventually meet at a certain point.