Implement Queue Using Stack

Problem Statement

The task here is to implement a First In First Out queue using Stacks. The queue should support all functions such as push, pop, peek.

Examples:

Input
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]

Output
[null, null, null, 1, 1, false]

Explanation

MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false 

Before diving into the solution, let us first understand the basic difference between Stack and Queue.

Stack is Last in First Out data structure. Push and pop operations take place only through one end of the stack i.e. top(). It supports push, pop, peek operations.

Queue is First In First Out data structure. Push and pop operations take place through two ends of the queue. It supports enqueue, dequeue, peek operations.

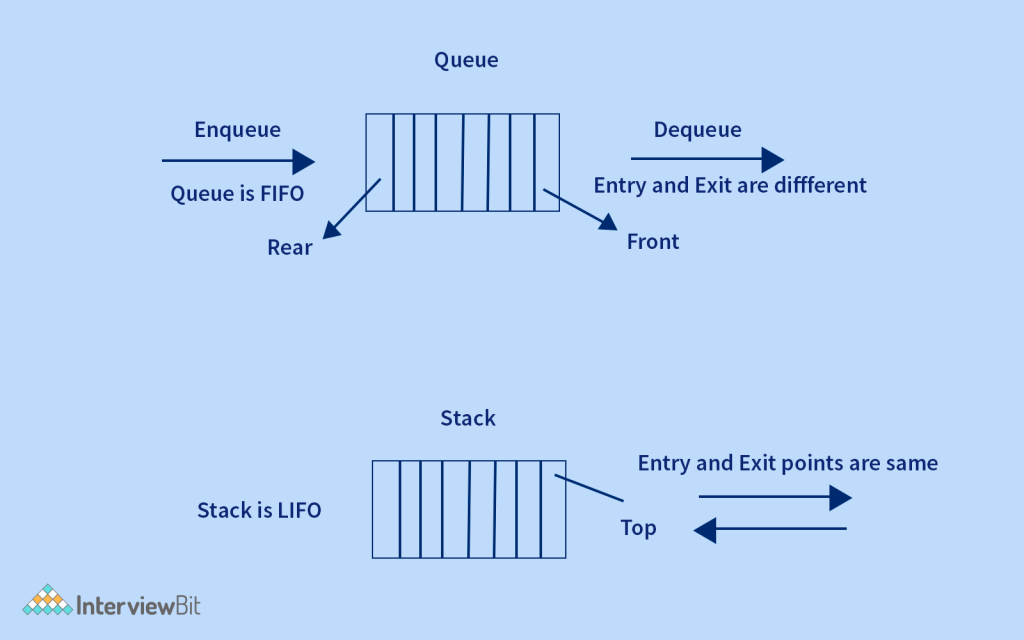
So, if you clearly observe, we would require two stacks to implement the queue, one for en queue and another for de queue operation.

Approach 1: Making enqueue operation costly

As discussed above, we know, in the queue, it follows a FIFO order, i.e., the element which gets in first, gets out first. Therefore, we need to devise a technique using stacks, such that the element which will be pushed will remain at the top.
Therefore, we will use a second stack for the same.

Algorithm

For enqueue

• Initialise two stacks S1 and S2.
• If S1 is empty, insert the element into S2.
• Else, push all the elements from S1 to S2.
• Push the element that needs to be inserted into S1.
• Push all the elements from S2 back to S1.

For dequeue

• If the stack S1 is empty, return -1.
• Else, return the top element of the stack. 

C++ Code

struct Queue {
  stack < int > s1, s2;
 
  void enQueue(int x) {
    while (!s1.empty()) {
      s2.push(s1.top());
      s1.pop();
    }
    s1.push(x);
    while (!s2.empty()) {
      s1.push(s2.top());
      s2.pop();
    }
  }
  int deQueue() {
    if (s1.empty()) {
      cout << "Q is Empty";
      exit(0);
    }
    int x = s1.top();
    s1.pop();
    return x;
  }
};

Java Code

static class Queue {
  static Stack < Integer > s1 = new Stack < Integer > ();
  static Stack < Integer > s2 = new Stack < Integer > ();
 
  static void enQueue(int x) {
    while (!s1.isEmpty()) {
      s2.push(s1.pop());
    }
    s1.push(x);
    while (!s2.isEmpty()) {
      s1.push(s2.pop());
    }
  }
  static int deQueue() {
    if (s1.isEmpty()) {
      System.out.println("Q is Empty");
      System.exit(0);
    }
    int x = s1.peek();
    s1.pop();
    return x;
  }
};

Python Code

class Queue:
    def __init__(self):
        self.s1 = []
        self.s2 = []
 
    def enQueue(self, x):
 
        while len(self.s1) != 0:
            self.s2.append(self.s1[-1])
            self.s1.pop()
 
        self.s1.append(x)
 
        while len(self.s2) != 0:
            self.s1.append(self.s2[-1])
            self.s2.pop()
 
    def deQueue(self):
 
        if len(self.s1) == 0:
            print("Q is Empty")
 
        x = self.s1[-1]
        self.s1.pop()
        return x

Time Complexity: O(N) for enqueue operation, O(1) for pop 
Space Complexity: O(N)

Approach 2: Making dequeue operation costly

Algorithm:

For enqueue

• Initialise two stacks S1 and S2.
• Push all the elements into S1.

For dequeue

• If the size of S1 and S2 is 0, return -1.
• Push all the elements to S2 from S1.
• Remove the top element of the stack S1.

C++ Implementation

struct Queue {
  stack < int > s1, s2;
  void enQueue(int x) {
    s1.push(x);
  }
  int deQueue() {
    if (s1.empty() && s2.empty()) {
      cout << "Q is empty";
      exit(0);
    }
    if (s2.empty()) {
      while (!s1.empty()) {
        s2.push(s1.top());
        s1.pop();
      }
    }
    int x = s2.top();
    s2.pop();
    return x;
  }
};

Java Implementation

 static class Queue {
  Stack < Integer > stack1;
  Stack < Integer > stack2;
}
static void push(Stack < Integer > top_ref, int new_data) {
  top_ref.push(new_data);
}
static int pop(Stack < Integer > top_ref) {
  if (top_ref.isEmpty()) {
    System.out.println("Stack Underflow");
    System.exit(0);
  }
  return top_ref.pop();
}
static void enQueue(Queue q, int x) {
  push(q.stack1, x);
}
static int deQueue(Queue q) {
  int x;
  if (q.stack1.isEmpty() && q.stack2.isEmpty()) {
    System.out.println("Q is empty");
    System.exit(0);
  }
  if (q.stack2.isEmpty()) {
    while (!q.stack1.isEmpty()) {
      x = pop(q.stack1);
      push(q.stack2, x);
    }
  }
  x = pop(q.stack2);
  return x;
}

Python Implementation

class Queue:
    def __init__(self):
        self.s1 = []
        self.s2 = []
 
    def enQueue(self, x):
        self.s1.append(x)
 
    def deQueue(self):
        if len(self.s1) == 0 and len(self.s2) == 0:
            print("Q is Empty")
            return
 
        elif len(self.s2) == 0 and len(self.s1) > 0:
            while len(self.s1):
                temp = self.s1.pop()
                self.s2.append(temp)
            return self.s2.pop()
 
        else:
            return self.s2.pop()

Time Complexity: O(1) for enqueue operation, O(N) for pop 
Space Complexity: O(N)

FAQs

Q. Which approach is more efficient? Making enqueue operation costly or dequeue operation costly?
A. Both the problems have the same time complexity, hence, we are free to use any one of them.

Q. What is a queue?
A. A queue is a data structure that follows the FIFO(first in first out) method, i.e. element which goes in first, comes out first.