Inorder Traversal Of A Binary Tree

What is Inorder Traversal?

It’s a technique of traversing over all nodes of the tree. In inorder traversal of a binary tree, the whole left subtree then the current node, and after that, we traverse the right subtree

Problem Statement

We have talked about binary trees in this section and not for the n-ary tree as we are not defined with the left or right child, so we can’t follow a manner of traversing, so these techniques are most effective in the binary trees.

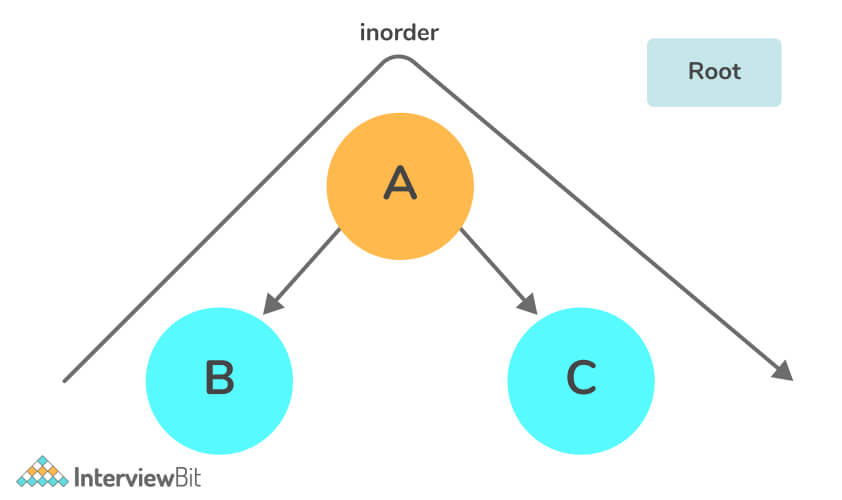
Example:

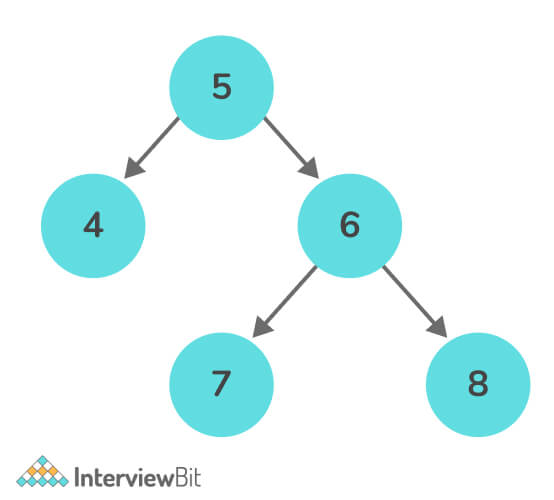
Inorder Traversal: 4 5 7 6 8

Inorder Traversal With Recursion

In inorder the flow of traversing will be left_subtree -> current -> right_subtree.

• Base case: we have to check whether the node is present or not, i.e. not NULL.
• Traverse left the child with a recursive call passing the current->left as root.
• After returning from this call, the node would be leftmost so that we can store this first node of the inorder traversal.
• Now we have the left child, and the root now makes a recursive call for the right subtree.

C++ Code Implementation

void inorder(Tree* root) {
   if(!root)return;
   inorder(root->left,ans);
   cout<<root->data<<endl;
   inorder(root->right,ans);
}

Python Code Implementation

def InOrder(root):
    if root:
        # recursive call for left child
        InOrder(root.left)
        print(root.val),
        # recursive call for the right child
        InOrder(root.right)

Java Code Implementation

void InOrder(Tree root) {
   if (root == null)
     return;
   InOrder(root.left);
   System.out.print(root.key + " ");
   InOrder(root.right);
}

• Time complexity: O(N), Where N is no of nodes in the tree.
• Space complexity: O(1)

Inorder Traversal Iterative

By this method, we iteratively traverse the trees. In this, we have to use the stack data structure.

• Create a stack to store the values while traversing to the leftmost child.
• Create a current node as root.
• Traverse till the current node is not null or we have elements in our stack to process
• As in order, we need the leftmost child first, so traverse to get the leftmost child in a nested loop.
• Pop the top element from the stack and print it as it’s the first node we needed and so on.
• As our curr will be null after returning from the nested loop, make our current to the right of the top element as the left subtree, and the current node of the top element of the stack is processed, and now we have to traverse the right subtree.

C++ Code Implementation

void inOrder(struct Tree *root) {
    stack<Tree *> s;
    Tree *curr = root;
    while (curr != NULL || s.empty() == false)
    {
        while (curr !=  NULL)
        {
            s.push(curr);
            curr = curr->left;
        }
        cout << s.top()->data << " ";
        curr = s.top()->right;
        s.pop();
    } 
}

Java Code Implementation

void inorder() {
  if (root == null)
    return;
  Stack < Tree > s = new Stack < Tree > ();
  Tree curr = root;
  while (curr != null || s.size() > 0) {
    while (curr != null) {
      curr = curr.left;
    }
    curr = s.pop();
    System.out.print(curr.data + " ");
    curr = curr.right;
  }
}

Python Code Implementation

def inOrder(root):

    current = root
    stack = []
    while True:
        iterative
        if current is not None:
            stack.append(current)
            current = current.left
        elif stack:
            current = stack.pop()
            print(current.data, end=" ")
            current = current.right
        else:
            break

• Time complexity: O(N), Where N is no of nodes in the tree.
• Space complexity: O(N).

Inorder Traversal in Binary Search Tree: We can do inorder traversal in the binary search tree and find that the result will always be in the sorted order because of the property of the binary search tree that the left child is always smaller than the root and root will be smaller than the right child.

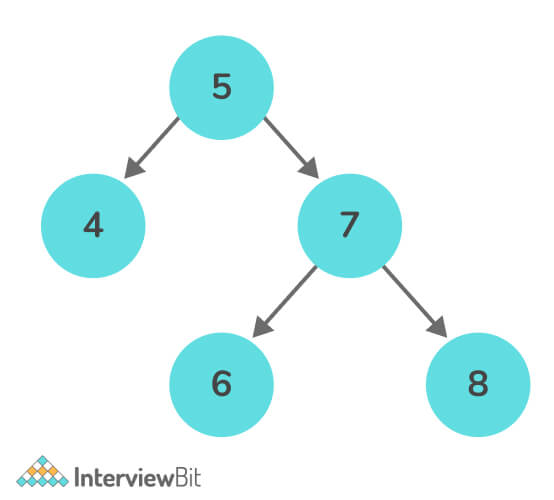
Considering this BST we can see that the in-order traversal of this tree will be

In-order – 4 5 6 7 8

Practice Questions

• Inorder Traversal Problem
• Inorder Traversal Of Cartesian Tree

Frequently Asked Questions

Q.1: How do you find the inorder on a traversal?

Ans: We can find the inorder using recursion or traversing the tree iteratively using a stack.

Q.2: Is inorder traversal o(n)?

Ans: Yes, but n here is the number of nodes in the tree.

Q.3: Which tree traversal is most efficient?

Ans: From Inorder, preorder, and postorder it depends according to your requirement as all the traversals are similar in terms of time complexities. Iterative is more efficient than recursive.

Q.4: What is in-order traversal used for?

Ans: It is used to traverse the tree in a given manner and use it according to our requirements and store it in other data structures or containers.

Additional Resources

• Binary Tree
• Top view of Binary Tree
• Diameter of a Binary Tree
• Bottom View of Binary Tree
• Level Order Traversal of Binary Tree
• Left View of a Binary Tree