Interleaving Strings (C, Java, and Python Code)

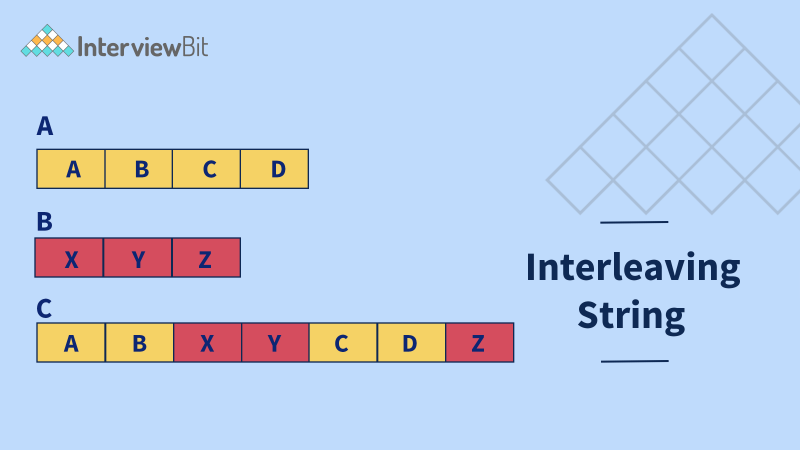
Given three strings S1, S2 and S3. The task is to check whether the string S3 can be formed by an interleaving of strings S1 and S2.
S3 is said to be interleaving S1 and S2 if it contains all the characters of S1 and S2 and the order is preserved.

Examples:

Input:
s1 = “aabcc”
s2 = “dbbca”
s3 = “aadbbcbcac”       
Output: True
Explanation:

Input:
s1 = “aabcc”
s2 = “dbbca”
s3 = “aadbbbaccc”        

Output: False

Approach 1: Brute Force

The most basic approach to solve this problem is to simply consider all possible strings of S1 and S2. If you observe carefully, there are two ways that needs to be taken care of:

• If S3[0] == S1[0], move to the next characters and recursively iterate the rest of the string of S1.
• If S3[0] == S2[0],  move to the next characters and recursively iterate the rest of the string of S2.

Algorithm:

• The base case of the recursive function is when the strings S1, S2 and S3 are empty.
• For the rest of the function, check whether S3[0] == S1[0], then recursively traverse for S1[1…N]. 
• Similarly, if S3[0] == S2[0], then recursively traverse for S2[1…N].

Implementation of the Approach:

C++ Code

bool isInterleaving(string X, string Y, string S) {
  if (!X.length() && !Y.length() && !S.length()) {
    return true;
  }
 
  if (!S.length()) {
    return false;
  }
 
  if (X.length() && S[0] == X[0]) {
    return isInterleaving(X.substr(1), Y, S.substr(1));
  }
 
  if (Y.length() && S[0] == Y[0]) {
    return isInterleaving(X, Y.substr(1), S.substr(1));
  }
 
  return false;
}

Java Code

public static boolean isInterleaving(String X, String Y, String S) {
  if (X.length() == 0 && Y.length() == 0 && S.length() == 0) {
    return true;
  }
 
  if (S.length() == 0) {
    return false;
  }
 
  if (X.length() != 0 && S.charAt(0) == X.charAt(0)) {
    return isInterleaving(X.substring(1), Y, S.substring(1));
  }
 
  if (Y.length() != 0 && S.charAt(0) == Y.charAt(0)) {
    return isInterleaving(X, Y.substring(1), S.substring(1));
  }
 
  return false;
}

Python Code

def isInterleaving(X, Y, S):
    if not X and not Y and not S:
        return True
 
    if not S:
        return False
 
    if X and S[0] == X[0]:
        return isInterleaving(X[1:], Y, S[1:])
 
    if Y and S[0] == Y[0]:
        return isInterleaving(X, Y[1:], S[1:])
 
    return False

Time Complexity: O(2^(N+M)), where N and M is the length of the string S1 and S2.

Space Complexity: O(N + M), for the recursive stack.

Approach 2: Dynamic Programming

In the previous approach, if you observe carefully, there were many overlapping subproblems which we were calculating again and again.

For example :

To avoid repetitive calculations, the idea is to use Dynamic Programming to solve the problem. The DP table is built as follows. Consider the following example:

Algorithm:

• Create a 2D dp array of size N X M, where N is the size of S1 and M is the size of S2.
• Run a nested loop from i = 0 till i = N+1 and j = 0 till j =  M + 1 and fill the table as follows:
  • If i == 0 and j == 0:
    • Dp[i][j] = True
  • Else if i == 0 and S2[j – 1] == S3[i + j – 1]:
    • Dp[i][j] = dp[i][j – 1] + 1
  • Else if j == 0 and S1[j – 1] == S3[i + j – 1]:
    • Dp[i][j] = dp[i – 1][j] + 1
  • Else:
    • (DP[i-1][j] and S1[i-1] == S3[i+j-1] ) or (DP[i][j-1] and S2[j-1] == S3[i+j-1] )
• Return dp[N][M]

Implementation of the Approach:

C++ Code

bool isInterleaving(string X, string Y, string S) {
  int M = X.size();
  int N = Y.size();
 
  if (M + N != S.size()) {
    return false;
  }
 
  bool T[M + 1][N + 1];
 
  for (int i = 0; i <= M; i++) {
    for (int j = 0; j <= N; j++) {
      if (i == 0 && j == 0) {
        T[i][j] = true;
      } else if (i and j and X[i - 1] == S[i + j - 1] and Y[j - 1] == S[i + j - 1]) {
        T[i][j] = T[i - 1][j] || T[i][j - 1];
      } else if (i and X[i - 1] == S[i + j - 1]) {
        T[i][j] = T[i - 1][j];
      } else if (j and Y[j - 1] == S[i + j - 1]) {
        T[i][j] = T[i][j - 1];
      }
    }
  }
  return T[M][N];
}

Java Code

 public static boolean isInterleaving(String X, String Y, String S) {
  int M = X.length();
  int N = Y.length();
  if (M + N != S.length()) {
    return false;
  }
  boolean[][] T = new boolean[M + 1][N + 1];
  for (int i = 0; i <= M; i++) {
    for (int j = 0; j <= N; j++) {
      if (i == 0 && j == 0) {
        T[i][j] = true;
      } else if (i != 0 && j != 0 && X.charAt(i - 1) == S.charAt(i + j - 1) &&
        Y.charAt(j - 1) == S.charAt(i + j - 1)) {
        T[i][j] = T[i - 1][j] || T[i][j - 1];
      } else if (i != 0 && X.charAt(i - 1) == S.charAt(i + j - 1)) {
        T[i][j] = T[i - 1][j];
      } else if (j != 0 && Y.charAt(j - 1) == S.charAt(i + j - 1)) {
        T[i][j] = T[i][j - 1];
      }
    }
  }
  return T[M][N];
}

Python Code

def isInterleaving(X, Y, S):
    M, N = len(X), len(Y)
    if M + N != len(S):
        return False
 
    T = [[False for x in range(N + 1)] for y in range(M + 1)]
 
    for i in range(0, M + 1):
        for j in range(0, N + 1):
 
            if i == 0 and j == 0:
                T[i][j] = True
 
            elif i and j and X[i - 1] == S[i + j - 1] and Y[j - 1] == S[i + j - 1]:
                T[i][j] = T[i - 1][j] or T[i][j - 1]
 
            elif i and X[i - 1] == S[i + j - 1]:
                T[i][j] = T[i - 1][j]
 
            elif j and Y[j - 1] == S[i + j - 1]:
                T[i][j] = T[i][j - 1]
 
    return T[M][N]

Time Complexity: O(N*M), where N and M is the length of the string S1 and S2.

Space Complexity: O(N * M), since dp array is used.

Practice Questions:

Interleaving Strings

FAQ

• What are the two types of possibilities for interleaving?
  The two types of possibilities are as follows:
  1. If S3[0] == S1[0], move to the next characters and recursively iterate the rest of the string of S1.

If S3[0] == S2[0],  move to the next characters and recursively iterate the rest of the string of S2.