Problem Statement
Given an integer array, A[] and an integer K. The task is to return the Kth largest element in an array.
Examples:
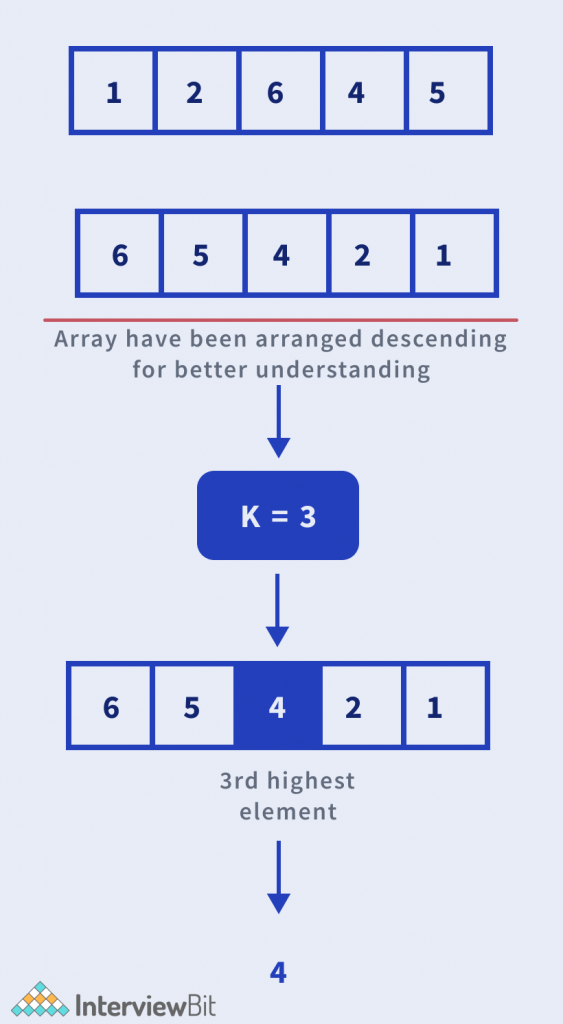
Input: A[] = {1, 2, 6, 4, 5}, K = 3
Output: 4
Explanation: Provided in image above
Confused about your next job?
Input: A[] = {3, 2, 1, 5, 6, 4}, K = 2
Output: 5
Approach 1: Sort
The most naive approach to solve this problem is to simply sort the given array in descending order and return the Kth element from the beginning of the array.
C++ Code
int kthLargest(vector < int > & arr, int size, int K) {
sort(arr.begin(), arr.end(), greater < int > ());
return arr[K - 1];
}Java Code
static int kthLargest(ArrayList < Integer > arr, int size, int K) {
Collections.sort(arr, Collections.reverseOrder());
return arr.get(K - 1);
}Python Code
def kthLargest(arr, size, k):
arr = sorted(arr, reverse=True)
return arr[k - 1]Time Complexity: O(NlogN), where N is the size of the array.
Space Complexity: O(1), since no additional space is used.
Approach 2: Heap
The previous approach of sorting and finding the Kth largest element is costly. Since the task is to return the Kth largest element, the idea would be to maintain a data structure that keeps the elements of the array in sorted order, along with reducing the time complexity.
The idea is to use a max-heap. Since max-heap keeps all the elements in sorted order, the problem simply converts to print the Kth element of the max-heap.
Let us try to understand this with the help of an example.
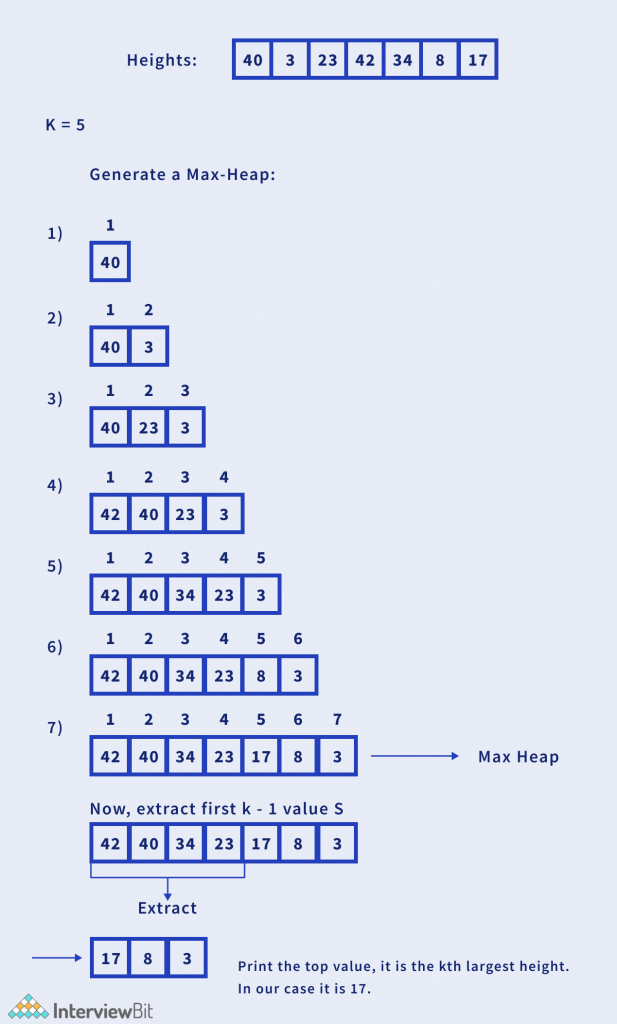
Algorithm :
- Initialise a max-heap.
- Insert all the elements of the given array into the max heap.
- Extract the first K – 1 elements from the heap.
- Print the top element of the max heap.
C++ Code
int kthLargest(vector < int > & arr, int size, int K) {
priority_queue < int > pq;
int val;
for (int i = 0; i < size; i++) {
pq.push(arr[i]);
}
int l = K - 1;
while (l > 0) {
pq.pop();
l--;
}
return pq.top();
}Java Code
static int kthLargest(ArrayList < Integer > arr, int size, int K) {
PriorityQueue < Integer > pq = new PriorityQueue < Integer > (Collections.reverseOrder());
for (int i = 0; i < size; i++) {
pq.add(arr.get(i));
}
int l = K - 1;
while (l > 0) {
pq.poll();
l = l - 1;
}
return pq.peek();
}Python Code
import heapq
def kthLargest(arr, size, k):
pq = []
for i in range(size):
heapq.heappush(pq, -1 * arr[i])
l = k - 1
while l > 0:
heapq.heappop(pq)
l = l - 1
return -1 * pq[0]Time Complexity: O(K + (N – K) * log(K) ), where N is size of the array.
Space Complexity: O(K), since the heap is used.
Approach 3: Using Quick Select
The approach is to use a quick select approach. This method is very similar to the quick sort approach.
It can be clearly observed that Kth largest element is the same as (N – K)th smallest element, where N is the size of the given array. Therefore, we can apply the Kth smallest approach to this problem.
Firstly, a pivot element must be chosen, similar to what we do in quicksort. It can be done using the partition algorithm.
Remind: In the partition algorithm, all elements are compared to the pivot element, and the elements less than the pivot are moved towards the left side and greater are moved toward the right.
Now, since the array has been divided into two parts, ignore one part and simply search for N – Kth element in the other part.
Let us understand this with an example:
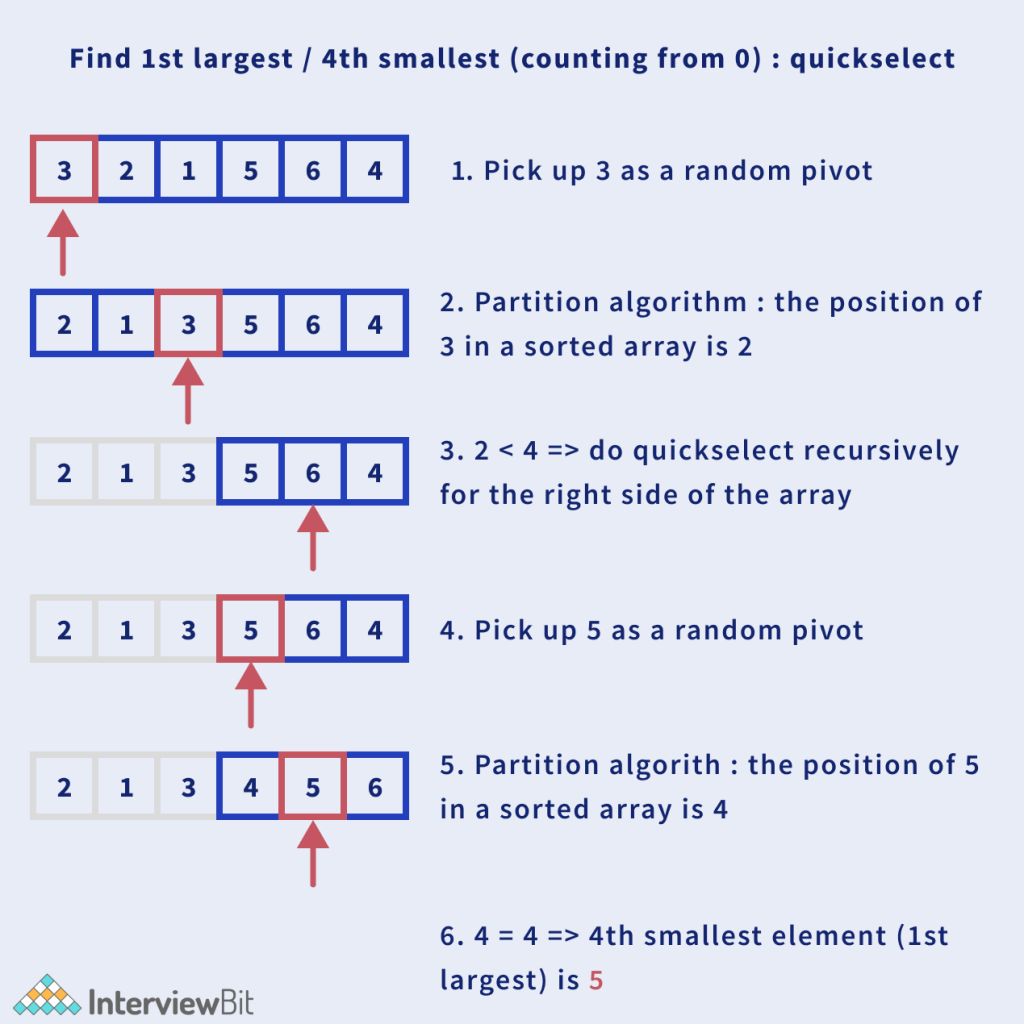
Algorithm:
- Choose any random element of the array as pivot.
- Use the partition algorithm to partition the array into two parts and place the pivot element in its correct position, idx.
- Now, since, all elements to the left of pivot are smaller and to the right of pivot are larger, compare the value of idx with N – K and recursively choose the part of the array to find the Kth largest element of the aray.
C++ Code
In CPP, there is an inbuilt reverse function in the algorithm header file, which when accessed can reverse string/array.
int findKthLargest(int nums[], int k) {
if (nums.size() == 1) {
return nums[0];
}
int lo = 0;
int hi = nums.length - 1;
int targetIndex = nums.length - k;
while (lo <= hi) {
int pivot = partition(nums, lo, hi);
if (pivot < targetIndex) {
lo = pivot + 1;
} else if (pivot > targetIndex) {
hi = pivot - 1;
} else {
return nums[pivot];
}
}
throw null;
}
int partition(int[] nums, int lo, int hi) {
int pivotVal = nums[hi];
int wall = lo;
for (int i = lo; i < hi; i++) {
if (nums[i] < pivotVal) {
swap(nums, wall, i);
wall++;
}
}
swap(nums, wall, hi);
return wall;
}
void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}Java Code
int[] nums;
public void swap(int a, int b) {
int tmp = this.nums[a];
this.nums[a] = this.nums[b];
this.nums[b] = tmp;
}
public int partition(int left, int right, int pivot_index) {
int pivot = this.nums[pivot_index];
swap(pivot_index, right);
int store_index = left;
for (int i = left; i <= right; i++) {
if (this.nums[i] < pivot) {
swap(store_index, i);
store_index++;
}
}
swap(store_index, right);
return store_index;
}
public int quickselect(int left, int right, int k_smallest) {
if (left == right)
return this.nums[left];
Random random_num = new Random();
int pivot_index = left + random_num.nextInt(right - left);
pivot_index = partition(left, right, pivot_index);
if (k_smallest == pivot_index)
return this.nums[k_smallest];
else if (k_smallest < pivot_index)
return quickselect(left, pivot_index - 1, k_smallest);
return quickselect(pivot_index + 1, right, k_smallest);
}
public int findKthLargest(int[] nums, int k) {
this.nums = nums;
int size = nums.length;
return quickselect(0, size - 1, size - k);
}Python Code
def findKthLargest(nums, k):
def partition(left, right, pivot_index):
pivot = nums[pivot_index]
nums[pivot_index], nums[right] = nums[right], nums[pivot_index]
store_index = left
for i in range(left, right):
if nums[i] < pivot:
nums[store_index], nums[i] = nums[i], nums[store_index]
store_index += 1
nums[right], nums[store_index] = nums[store_index], nums[right]
return store_index
def select(left, right, k_smallest):
if left == right:
return nums[left]
pivot_index = random.randint(left, right)
pivot_index = partition(left, right, pivot_index)
if k_smallest == pivot_index:
return nums[k_smallest]
elif k_smallest < pivot_index:
return select(left, pivot_index - 1, k_smallest)
else:
return select(pivot_index + 1, right, k_smallest)
return select(0, len(nums) - 1, len(nums) - k)Time Complexity: O(N), where N is the size of the array
Space Complexity: O(1), since no extra space is used.
Practice Questions
Kth Smallest Element in the Array
FAQs
- Can a min-heap be used to solve Kth largest element?
Yes, just like max heap, a min-heap can also be used to find the Kth largest element. - What is the most efficient approach to solve the Kthlargest element?
The quick select approach is the most efficient approach to solve the problem. The time complexity is O(N)







 Join WhatsApp Group
Join WhatsApp Group


