Longest Common Substring

Problem Statement

Given two strings, the task is to find the longest common substring present in the given strings in the same order.

The substring is a contiguous sequence of characters within a string. For example, “bit” is a substring of the string “Interviewbit”.

Example:

Input s1: “dadef”
s2: “adwce”
Output: 2
Explanation: Substring “ad” of length 2 is the longest.

Input s1: “abcdxyz”
s2: “xyzabcd”
Output: 4
Explanation: Substring “abcd” of length 4 is the longest.

Simple Approach

The simple approach checks for every substring of sequence 1 whether it is also a substring in sequence 2.

Sequence S1 and S2 with length n and m respectively

• Find all the substrings of sequence 1 in O(n^2)
• Iterate through sequence 2 and check whether the current substring is a substring of this string in O(m)
• Maximize the length of all the common substrings.

C++ Code of Simple Approach

void lcsubstr(string str1,string str2)
{
      int ans = 0;

	for (int i = 0; i < str1.length(); i++) 
	{
         for (int j = 0; j < str2.length(); j++) {
		int k = 0;
		while ((i + k) < str1.length() && (j + k) < str2.length() 
				&& str1[i + k] == str2[j + k]) 
		{
			k = k + 1;
		}

		ans = max(ans, k);
	   }
	}
      return ans;
}

Java Code of Simple Approach

public static int lcsubstr(string str1, string str2){
	int ans = 0;

	for (int i = 0; i < str1.length(); i++) 
	{
         for (int j = 0; j < str2.length(); j++) {
		int k = 0;
		while ((i + k) < str1.length() && (j + k) < str2.length() 
				&& str1.charAt(i + k) == str2.charAt(j + k)) 
		{
			k = k + 1;
		}

		ans = Math.max(ans, k);
	   }
	}
      return ans;
  }

Python Code of Simple Approach

def lcsubstr(str1, str2):
    	ans = 0;

	for i in range(len(str1)):
         for j in range(len(str2)):
		k = 0;
		while ((i + k) < len(str1) and (j + k) < len(str2) 
				and str1[i + k] == str2[j + k]): 
			k = k + 1;

		ans = max(ans, k);
      return ans;

Time complexity: O(n^2 * m), Where n and m are the lengths of sequences.
Space complexity: O(1)

Recursive Approach

In the recursive approach, the idea is to recursively match characters of both the sequences and maximize in case the characters are the same.

Algorithm

• Initialise a variable res, to count the longest common substring.
• Let i and j be the index of the str1 and str2 pointing to the last character of both the strings.
• If both the characters are the same, i.e. str1[i] == str2[j], increment the value of res by 1.
• Proceed to match the remaining characters, by decrementing the pointers i and j each time the characters don’t match.
• Maximize the value of count for every step.
• Repeat the above process, until we reach the starting of both strings.

Longest Common Substring C++

    int solve(int i, int j, int count, string str1, string str2)
    {
 
        if (i == 0 || j == 0)
        {
            return count;
        }
 
        if (str1[i - 1] == str2[j - 1])
        {
            count = solve(i - 1, j - 1, count + 1, str1, str2);
        }
        int count1 = solve(i, j - 1, 0, str1, str2);

        int count2 = solve(i - 1, j, 0, str1, str2);

        count = max({count, count1,count2});
        return count;
    }
    void lcsubstr(){
        int ans = solve(N, M, 0, str1, str2);
        return ans;
    }

Longest Common Substring Java

 static int solve(int i, int j, int count)
    {
 
        if (i == 0 || j == 0)
        {
            return count;
        }
 
        if (str1.charAt(i - 1) == str2.charAt(j - 1))
        {
            count = solve(i - 1, j - 1, count + 1, str1, str2);
        }

        int count1 = solve(i, j - 1, 0, str1, str2);

        int count2 = solve(i - 1, j, 0, str1, str2);

        count = Math.max(count,Math.max(count1,count2));

        return count;
    }
    static int lcsubstr(){
        int ans = solve(N, M, 0, str1, str2);
        return ans;
    }

Longest Common Substring Python

def solve(i, j, count, str1, str2):
        if i == 0 or j == 0:
            return count;
 
        if str1[i - 1] == str2[j - 1]:
            count = solve(i - 1, j - 1, count + 1, str1, str2);

        count1 = solve(i, j - 1, 0);

        count2 = lcs(i - 1, j, 0);

        count = max({count, count1,count2});
        return count;
def lcsubstr():
     ans = solve(N, M, 0, str1, str2);
     return ans;

Time complexity: O(3 ^(n*m)), where n and m are the lengths of sequences.
Space complexity: O(max(n, m))

Dynamic Programming Appraoch

The longest common substring can be efficiently calculated using the dynamic programming approach.

The idea is to calculate the longest common suffix for all substrings of both sequences.

Consider the below example –
str1 = “ABCXYZAY”
str2 =” “XYZABCB”

The longest common substring is “XYZA”, which is of length 4.

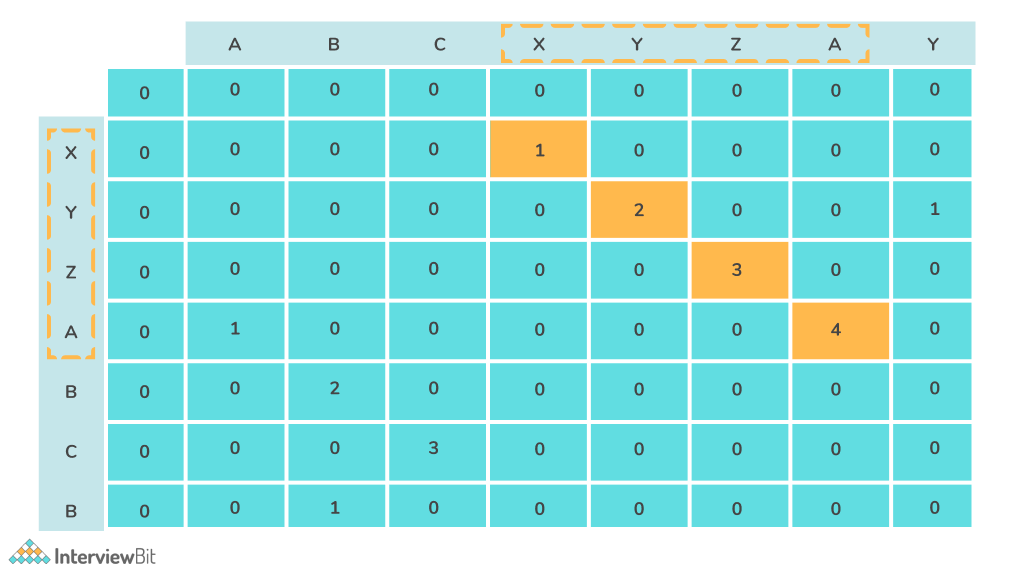
Algorithm:

• Create a dp array of size N * M, where N and M denote the length of the sequences.
• Iterate over the string str1 and str2 using a nested loop.
• The below conditions follows:
  • If i == 0 or j == 0, dp[i][j] = 0
  • If str1[i] == str2[j], dp[i][j] = 1 + dp[i – 1][j – 1]
• Keep a track of the maximum value obtained so far.
• Return the maximum value.

C++ Implementation

int LCSubStr(string str1, string str2, int N, int M)
{
    int LCSuff[N + 1][M + 1];
    int mx = 0;    
    for (int i = 0; i <= N; i++)
    {
        for (int j = 0; j <= M; j++)
        {
              if (i == 0 || j == 0){
                LCSuff[i][j] = 0;
              }
 
            else if (str1[i - 1] == str2[j - 1]) {
                LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;
                mx = max(mx, LCSuff[i][j]);
            }
            else
                LCSuff[i][j] = 0;
        }
    }
    return mx;
}

Java Implementation

static int LCSubStr(char str1[], char str2[], int N, int M){
        int LCStuff[][] = new int[N + 1][M + 1];
       
        int mx = 0;

        for (int i = 0; i <= N; i++)
        {
            for (int j = 0; j <= M; j++)
            {
                if (i == 0 || j == 0)
                    LCStuff[i][j] = 0;
                else if (str1[i - 1] == str2[j - 1])
                {
                    LCStuff[i][j]
                        = LCStuff[i - 1][j - 1] + 1;
                    mx = Integer.max(mx,
                                         LCStuff[i][j]);
                }
                else
                    LCStuff[i][j] = 0;
            }
        }
        return mx;
    }

Python Implementation

def LCSubStr(str1, str2, N, M):
 
    LCSuff = [[0 for k in range(M+1)] for l in range(N+1)]
    mx = 0
    for i in range(N + 1):
        for j in range(M + 1):
            if (i == 0 or j == 0):
                LCSuff[i][j] = 0
            elif (str1[i-1] == str2[j-1]):
                LCSuff[i][j] = LCSuff[i-1][j-1] + 1
                mx = max(result, LCSuff[i][j])
            else:
                LCSuff[i][j] = 0
    return mx

Time complexity: O(n*m), Where n and m are the lengths of sequences.
Space complexity: O(n*m)

Practice Question

Longest Common Prefix

Frequently Asked Questions

Q.1: How do you find the longest common substring?

Ans: The most efficient method is to use the dynamic programming approach of storing sub-problems.

Q.2: What is the time complexity of the longest common substring?

Ans: It depends if we don’t use dynamic programming to store subproblems then it would be O(3^(n+m)) time and O(1) space and using dynamic programming its O(nm) time and O(nm) space where n,m are lengths of sequence.

Q.3: What is the time complexity of finding the longest non-repeated substring?

Ans: The time complexity of finding the longest non-repeated substring is O(n).