Maximum Product Subarray Problem

Given an array A[] of N positive integers. The task is to find a non empty subarray having the largest product and return the product.

Examples:

Input: A[] = [2, 3, -2, 4]
Output: 6
Explanation: The maximum product subarray is [2, 3] = 6

Input:  A[] = [-2, 0, -1]

Output: 0

Approach 1: Brute Force

A simple approach to solve this problem is to find all possible subarrays of the given input array and maximize the product of all subarrays found so far.

Algorithm :

• Initialise a variable result = A[0]  to store the maximum product.
• Run two nested loops from i = 0 till N – 1 and j  from i + 1 till N and for each subarray A[i….j], find the product of the subarray.
• Update and maximize result.

Implementation of the Approach:

C++ Code

bool isOverlap(int minS, int maxE, vector<int> interval)
{
    if (minS > interval[1] || maxE < interval[0])
    {
        return false;
    }
 
    return true;
}
 
int maxProduct(vector<int> nums) {
  if (nums.size() == 0) return 0;
 
  int result = nums[0];
 
  for (int i = 0; i < nums.size(); i++) {
    int accu = 1;
    for (int j = i; j < nums.size(); j++) {
      accu *= nums[j];
      result = max(result, accu);
    }
  }
  return result;
}

Java Code

public int maxProduct(int[] nums) {
  if (nums.length == 0) return 0;
 
  int result = nums[0];
 
  for (int i = 0; i < nums.length; i++) {
    int accu = 1;
    for (int j = i; j < nums.length; j++) {
      accu *= nums[j];
      result = Math.max(result, accu);
    }
  }
 
  return result;
}

Python Code

def maxProduct(nums):
    if len(nums) == 0:
        return 0
 
    result = nums[0]
 
    for i in range(len(nums)):
        accu = 1
        for j in range(i, len(nums)):
            accu *= nums[j]
            result = max(result, accu)
 
    return result

Time Complexity: O(N^2), where N is total size of the array

Space Complexity: O(1), as no extra space is used

Approach 2: Dynamic Programming

If we observe clearly, the maximum product will always lie either from the starting of the array or from the end of the array.

To summarise, we have four possible options.

You might think, what if the maximum product lies somewhere in the middle of the array. Let us prove this using contradiction.

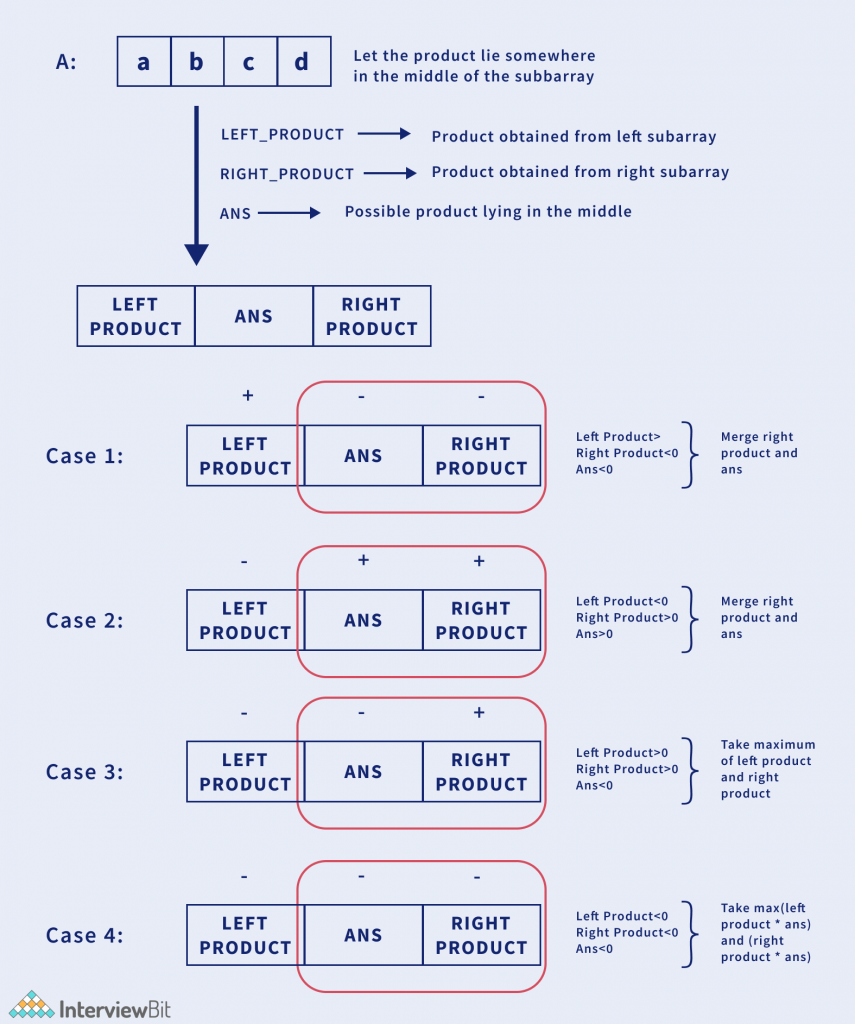
In the above example, it has been proved, that the maximum product lies either on the left end or the right end.

Algorithm :

• Initialise a variable result = A[0]  to store the maximum product.
• Initialise two variables max_so_far and min_so_far with A[0], which stores the maximum and minimum product obtained so far
• Traverse the input array and for negative element swap max_so_far and min_so_far.
• Maximize max_so_far and update it with max_so_far * A[i]
• Minimise min_so_far and update it with min_so_far * A[i]
• Update result with maximum of max_so_far and min_so_far.
• Return result.

Implementation of the Approach:

C++ Code

vector < vector < int >> merge(vector < vector < int >> & intervals) {
  sort(intervals.begin(), intervals.end());
 
  vector < vector < int >> merged;
  for (auto interval: intervals) {
    if (merged.empty() || merged.back()[1] < interval[0]) {
      merged.push_back(interval);
    } else {
      merged.back()[1] = max(merged.back()[1], interval[1]);
    }
  }
  return merged;
}

Java Code

 int maxProduct(vector < int > nums) {
  if (nums.size() == 0) return 0;
 
  int max_so_far = nums[0];
  int min_so_far = nums[0];
  int result = max_so_far;
 
  for (int i = 1; i < nums.size(); i++) {
    int curr = nums[i];
    int temp_max = max(curr, Math.max(max_so_far * curr, min_so_far * curr));
    min_so_far = min(curr, Math.min(max_so_far * curr, min_so_far * curr));
 
    max_so_far = temp_max;
 
    result = max(max_so_far, result);
  }
 
  return result;
}

Python Code

def maxProduct(self, nums: List[int]) -> int:
    if len(nums) == 0:
        return 0
 
    max_so_far = nums[0]
    min_so_far = nums[0]
    result = max_so_far
 
    for i in range(1, len(nums)):
        curr = nums[i]
        temp_max = max(curr, max_so_far * curr, min_so_far * curr)
        min_so_far = min(curr, max_so_far * curr, min_so_far * curr)
 
        max_so_far = temp_max
 
        result = max(max_so_far, result)
 
    return result

Time Complexity: O(N), where N is total size of the array

Space Complexity: O(1), as no extra space is used.

Practice Questions:

Max Product Subarray

FAQ

• What if the input array has only positive integers?
  If the array contains just positive integers, the maximum product subarray is simply the product of all the integers.

• What is the most efficient approach to solve the maximum product subarray?
  The dynamic programming approach is the most efficient approach to solve the problem. The time complexity is O(N) and space complexity is O(1).