Problem Statement
Given an NxN Chessboard, we have to place N Queens such that they do not attack each other. (A queen can attack any square vertically, Horizontally, or diagonally).
Example of N Queen Problem :
Given, N = 8,
Confused about your next job?
One of the possible solution such that no queen attack any of the other queens,

Method 1 (Using Backtracking)
As we know we cannot place any two queens in the same row thus every queen will be placed in different rows. Now, we can place ith queen to ith row if the square we are placing in is safe to place due to the previously placed queens; if there are no such squares left we can backtrack and return false.
For every queen we are placing we have to check,
- There should be no queen in the same column,
- There should be no queen in the same row,
- There should be no queen in the same diagonal (upper left and right diagonal).
Note that we can eliminate the row search as we are already moving row-wise to place the queens thus there will be no other queen in the same row thus we can eliminate that search.
Code for the above implementation :
C++ Code Implementation
/* Function to print solution */
void printBoard(vector<vector<int>> chess)
{
int N = chess.size();
for (int i = 0; i < N; i++) {
for (int j = 0; j < N;j++) {
cout<<chess[i][j]<<" ";
}
cout<<endl;
}
}
bool isValid(vector<vector<int>> chess, int r, int c)
{
int N = chess.size();
/* Check this column only upward */
for (int i = 0; i < r; i++)
if (chess[i][c]==1)
return false;
/* Check upper diagonal on right side */
for (int i = r, j = c; j < N && i >= 0; i--, j++)
if (chess[i][j]==1)
return false;
/* Check upper diagonal on left side */
for (int i = r, j = c; i >= 0 && j >= 0; i--, j--)
if (chess[i][j]==1)
return false;
return true;
}
/* Recursive function for N-Queen Problem*/
bool recurNqueen(vector<vector<int>> chess, int r,int N)
{
/* if no queens are left to place
we return true. */
if (r >= N)
return true;
for (int i = 0; i < N; i++) {
/*Check if placing queen to chess[r][i] is valid.*/
if (isValid(chess, r, i)) {
/* Place this queen in chess[r][i] */
chess[r][i] = 1;
/* move ahead for next row */
if (recurNqueen(chess, r + 1,N))
return true;
/* Backtracking */
chess[r][i] = 0;
}
}
/* If the queen cannot be placed in any column for
the given row we return false.*/
return false;
}
void NQueen(int N)
{
/* creating chess board of NxN and initialising it with 0*/
vector<vector<int>> chess(N,vector<int>(N,0));
/*initialising the recursive function from 0th row*/
if (recurNqueen(chess, 0, N) == 0) {
/* if no solution exists the recursive function will end up
returning false.*/
cout<<"Solution Do not exist for "<<N<<" Queens ";
return;
}
/* else solution exists and printing out the solution*/
printBoard(chess);
return;
}
Java Code Implementation
static void printBoard(int chess[][],int N)
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(" " + chess[i][j] + " ");
}
System.out.println();
}
}
static boolean isValid(int chess[][], int r, int c,int N)
{
/* Check this column only upward */
for (int i = 0; i < r; i++)
if (chess[i][c]==1)
return false;
/* Check upper diagonal on right side */
for (int i = r, j = c; j < N && i >= 0; i--, j++)
if (chess[i][j]==1)
return false;
/* Check upper diagonal on left side */
for (int i = r, j = c; i >= 0 && j >= 0; i--, j--)
if (chess[i][j]==1)
return false;
return true;
}
/* Recursive function for N-Queen Problem*/
static boolean recurNqueen(int chess[][], int r,int N)
{
/* if no queens are left to place
we return true. */
if (r >= N)
return true;
for (int i = 0; i < N; i++) {
/*Check if placing queen to chess[r][i] is valid.*/
if (isValid(chess, r, i, N)) {
/* Place this queen in chess[r][i] */
chess[r][i] = 1;
/* move ahead for next row */
if (recurNqueen(chess, r + 1, N))
return true;
/* Backtracking */
chess[r][i] = 0;
}
}
/* If the queen cannot be placed in any column for
the given row we return false.*/
return false;
}
static void NQueen(int N)
{
/* creating chess board of NxN and initialising it with 0*/
int chess[][] = new int[N+1][N+1];
for(int i=0;i<N+1;i++){
for(int j=0;j<N+1;j++){
chess[i][j] = 0;
}
}
/*initialising the recursive function from 0th row*/
if (recurNqueen(chess, 0, N) == false) {
/* if no solution exists the recursive function will end up
returning false.*/
System.out.print("Solution Do not exist for " + N + " Queens. ");
return;
}
/* else solution exists and printing out the solution*/
printBoard(chess, N);
return;
}
Python Code Implementation
# Function to print solution
def printBoard(chess,N) :
for i in range(N):
for j in range(N):
print(chess[i][j],end=' ')
print()
def isValid( chess, r, c, N) :
# Check this column only upward
for i in range(r):
if chess[i][c]==1:
return False
# Check upper diagonal on right side
for i, j in zip(range(r, -1, -1),range(c, N, 1)):
if chess[i][j]==1:
return False
# Check upper diagonal on left side
for i, j in zip(range(r, -1, -1),range(c, -1, -1)):
if chess[i][j]==1:
return False
return True
# Recursive function for N-Queen Problem
def recurNqueen( chess, r, N):
# if no queens are left to place
# we return true.
if r >= N:
return True
for i in range(N):
# Check if placing queen to chess[r][i] is valid.
if isValid(chess, r, i, N) == True:
# Place this queen in chess[r][i]
chess[r][i] = 1
# move ahead for next row
if recurNqueen(chess, r + 1, N):
return True
# Backtracking
chess[r][i] = 0
# If the queen cannot be placed in any column for
# the given row we return false.
return False
def NQueen(N):
# creating chess board of NxN and initialising it with 0
chess = [[0 for i in range(N+1)] for j in range(N+1)]
# initialising the recursive function from 0th row
if recurNqueen(chess, 0, N) == 0:
# if no solution exists the recursive function will end up
# returning false.
print("Solution not found !!")
return
# else solution exists and printing out the solution*/
printBoard(chess, N)
- Time Complexity of the Above approach: O(N!).
Method 2 (A little optimisation)
In the above approach, we can make some of the observations based on the image below.
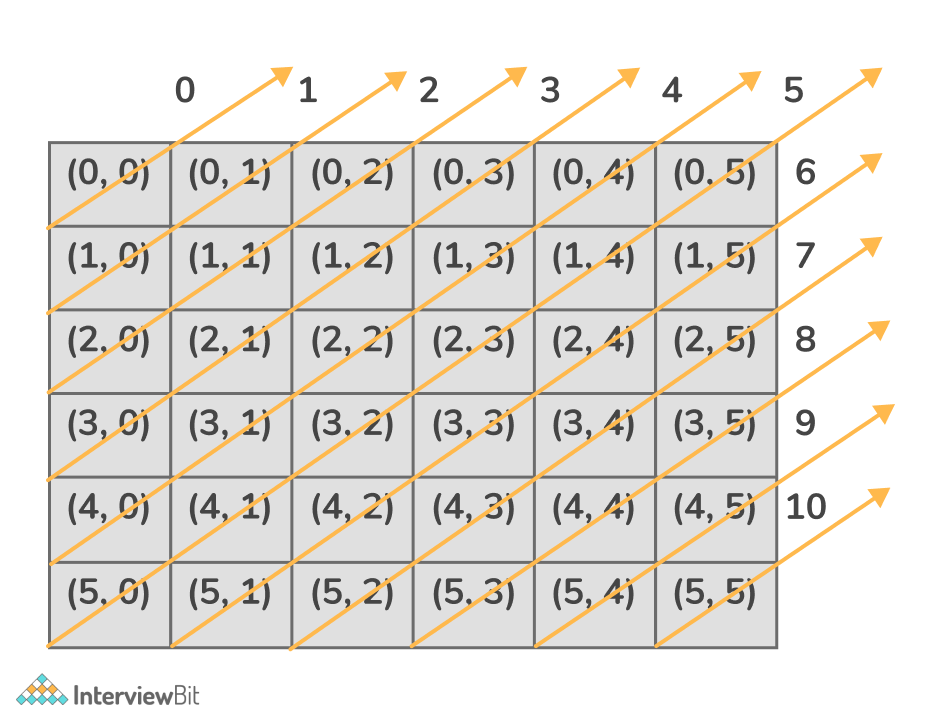
From the above image, we can clearly observe that every right diagonal can be represented as a sum of coordinates of the cells through which the diagonal passes.
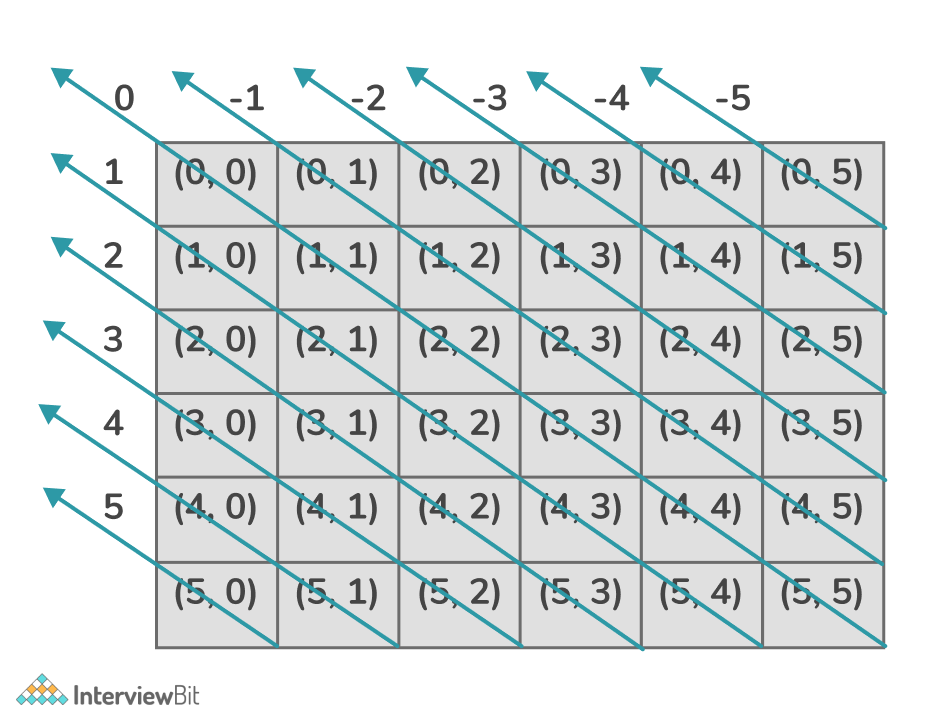
From the above image, we can observe that every left diagonal can be represented by the difference in the coordinates of the cells lying on the diagonal.
Thus using the same we can reduce our time by excluding the step for searching the whole diagonal using a loop instead we can create an array for the left, and right diagonals and columns to store if there exists a queen in them.
Code for the above optimization :
C++ Code Implementation
/*global vectors to store previously placed queens*/
vector<vector<int>> prevd;
vector<int> prevc;
/* Function to print solution */
void printBoard(vector<vector<int>> chess)
{
int N = chess.size();
for (int i = 0; i < N; i++) {
for (int j = 0; j < N;j++) {
cout<<chess[i][j]<<" ";
}
cout<<endl;
}
}
bool isValid(vector<vector<int>> chess, int r, int c)
{
int N = chess.size();
/* Check this column only upward */
if(prevc[c] == 1) return false;
/* Check upper diagonal on right side */
if(prevd[r+c][0] == 1) return false;
/* Check upper diagonal on left side */
if(prevd[r-c+N-1][1] == 1) return false;
return true;
}
/* Recursive function for N-Queen Problem*/
bool recurNqueen(vector<vector<int>> chess, int r,int N)
{
/* if no queens are left to place
we return true. */
if (r >= N)
return true;
for (int i = 0; i < N; i++) {
/*Check if placing queen to chess[r][i] is valid.*/
if (isValid(chess, r, i)) {
/* Place this queen in chess[r][i] and mark
the respective column , right and left diagonal. */
chess[r][i] = 1;
prevc[i] = 1;
prevd[r+i][0] = 1;
prevd[r-i+N-1][1] = 1;
/* move ahead for next row */
if (recurNqueen(chess, r + 1,N))
return true;
/* Backtracking */
chess[r][i] = 0;
prevc[i] = 0;
prevd[r+i][0] = 0;
prevd[r-i+N-1][1] = 0;
}
}
/* If the queen cannot be placed in any column for
the given row we return false.*/
return false;
}
void NQueen(int N)
{
/* creating chess board of NxN and initialising it with 0*/
vector<vector<int>> chess(N,vector<int>(N,0));
/*creating and initializing global vector to store answers
for prev diagonals and columns.*/
prevd.resize(2*N,vector<int> (2,0));
prevc.resize(N,0);
/*initialising the recursive function from 0th row*/
if (recurNqueen(chess, 0, N) == 0) {
/* if no solution exists the recursive function will end up
returning false.*/
cout<<"Solution Do not exist for "<<N<<" Queens ";
return;
}
/* else solution exists and printing out the solution*/
printBoard(chess);
return;
}
Java Code Implementation
/*global arrays to store previously placed queens*/
static int prevd[][];
static int prevc[];
/* Function to print solution */
static void printBoard(int chess[][],int N)
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.print(" " + chess[i][j] + " ");
}
System.out.println();
}
}
static boolean isValid(int chess[][], int r, int c,int N)
{
/* Check this column only upward */
if(prevc[c] == 1) return false;
/* Check upper diagonal on right side */
if(prevd[r+c][0] == 1) return false;
/* Check upper diagonal on left side */
if(prevd[r-c+N-1][1] == 1) return false;
return true;
}
/* Recursive function for N-Queen Problem*/
static boolean recurNqueen(int chess[][], int r,int N)
{
/* if no queens are left to place
we return true. */
if (r >= N)
return true;
for (int i = 0; i < N; i++) {
/*Check if placing queen to chess[r][i] is valid.*/
if (isValid(chess, r, i, N)) {
/* Place this queen in chess[r][i] */
chess[r][i] = 1;
prevc[i] = 1;
prevd[r+i][0] = 1;
prevd[r-i+N-1][1] = 1;
/* move ahead for next row */
if (recurNqueen(chess, r + 1, N))
return true;
/* Backtracking */
chess[r][i] = 0;
prevc[i] = 0;
prevd[r+i][0] = 0;
prevd[r-i+N-1][1] = 0;
}
}
/* If the queen cannot be placed in any column for
the given row we return false.*/
return false;
}
static void NQueen(int N)
{
/* creating chess board of NxN and initialising it with 0*/
int chess[][] = new int[N+1][N+1];
for(int i=0;i<N+1;i++){
for(int j=0;j<N+1;j++){
chess[i][j] = 0;
}
}
prevd = new int[2*N][2];
for(int i=0;i<2*N;i++){
prevd[i][0] = 0;
prevd[i][0] = 1;
}
prevc = new int[N];
for(int i=0;i<N+1;i++){
prevc[i] = 0;
}
/*initialising the recursive function from 0th row*/
if (recurNqueen(chess, 0, N) == 0) {
/* if no solution exists the recursive function will end up
returning false.*/
System.out.print("Solution Do not exist for " + N + " Queens. ");
return;
}
/* else solution exists and printing out the solution*/
printBoard(chess, N);
return;
}
Python Code Implementation
prevd = []
prevc = []
# Function to print solution
def printBoard(chess,N) :
for i in range(N):
for j in range(N):
print(chess[i][j],end=' ')
print()
def isValid( chess, r, c, N) :
# Check this column only upward
if prevc[c] == 1:
return False
# Check upper diagonal on right side
if prevd[r+c][0] == 1:
return False
# Check upper diagonal on left side
if prevd[r-c+N-1][1] == 1:
return False
return True
# Recursive function for N-Queen Problem
def recurNqueen( chess, r, N):
# if no queens are left to place
# we return true.
if r >= N:
return True
for i in range(N):
# Check if placing queen to chess[r][i] is valid.
if isValid(chess, r, i, N) == True:
# Place this queen in chess[r][i]
chess[r][i] = 1
prevc[i] = 1
prevd[r+i][0] = 1
prevd[r-i+N-1][1] = 1
# move ahead for next row
if recurNqueen(chess, r + 1, N):
return True
# Backtracking
chess[r][i] = 0
prevc[i] = 0
prevd[r+i][0] = 0
prevd[r-i+N-1][1] = 0
# If the queen cannot be placed in any column for
# the given row we return false.
return False
def NQueen():
N = 8
# creating chess board of NxN and initialising it with 0
chess = [[0 for i in range(N+1)] for j in range(N+1)]
prevd = [[0 for i in range(2*N)] for j in range(2)]
prevc = [0 for i in range(N+1)]
# initialising the recursive function from 0th row
if recurNqueen(chess, 0, N) == 0:
# if no solution exists the recursive function will end up
# returning false.
print("Solution not found !!")
return
# else solution exists and printing out the solution*/
printBoard(chess, N)
Practice Question
FAQs
Q.1: What is the algorithm used by the N- Queen problem?
Ans: To solve the N- Queen problem we use backtracking to reach the solution, however, we can add some optimisations one such solution is as discussed above.
Q.2: What is the Time Complexity of the N-Queen Problem?
Ans: The time complexity for the N-Queen problem solved using Backtracking is O(N!) where N denotes the number of Queens and dimensions of the chess board.




