Given an array A[] of N distinct integers. The task is to return the lexicographically greater permutation than the given arrangement. If no such arrangement is possible, return the array sorted in non-decreasing order.
Examples:
Input: A[] = [1, 2, 3]
Output: [1, 3, 2]
Explanation: The lexicographically greater permutation than A[] is [1, 3, 2]
Input: A[] = [4, 3, 2, 1]
Output: [1, 2, 3, 4]
Approach 1: Brute Force
A simple approach to solve this problem is to generate all the permutations of the given array and return the permutation which is just greater than the given array.
But this approach is very naive and won’t work for N > 10.
Time Complexity: O(N * N!), since total possible permutations are N!
Space Complexity: O(N), since the permutation is stored.
Approach 2: Linear Solution
In the last approach, we were trying to find all possible permutations. It takes an undeniably large time. So how can we improve it?
The problem can be solved using a simple trick.////////////////////
Let us understand this with the help of an example:
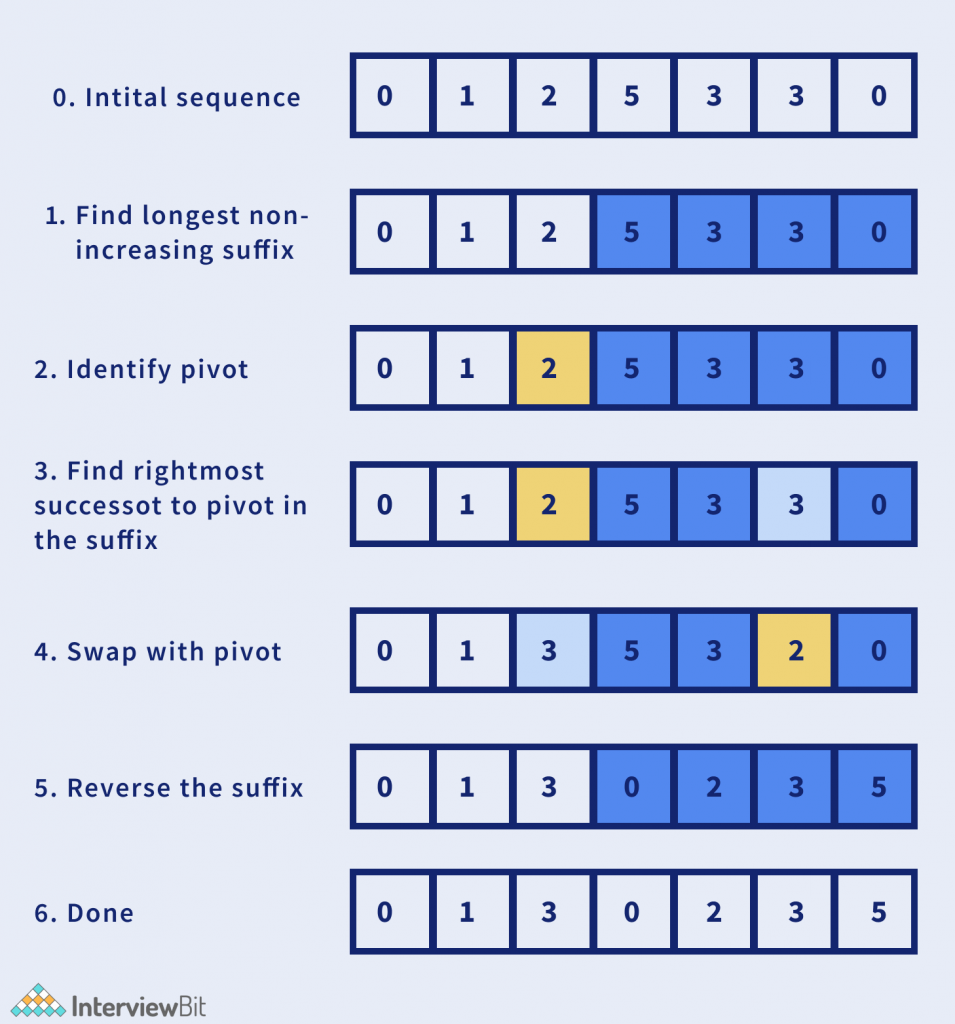
In the above example, we have followed four simple steps:
- Find the first index, say idx, where A[i] < A[i + 1].
- Find the first index, say ind, where A[i] > A[idx]
- Swap A[idx] and A[ind].
- Reverse all elements from idx + 1 till the end of the array.
But why does this work?
Recall the problem. We need to find the permutation just greater than the current arrangement given.
So, if we traverse from the end of the array, there will be an index where the current element is smaller than the previous element. This ensures that all the elements to its right are larger than the current element.
Now, to get the next greater arrangement, the most optimal approach would be to find the element which is just greater than the current found element.
So, now after swapping, we have found the pivot element. But we still have not got the required permutation. Therefore, simply sort the elements from the pivot till the end to get the required permutation.
The following example will make the approach more clear.
Algorithm :
- Traverse the array from end and find the first index, idx such that A[i] < A[i + 1].
- Again traverse the array from the end and find the first index, ind such that A[i] > A[idx].
- Swap A[idx] and A[ind].
- Reverse the array from idx + 1 till N.
- The base case would be, if the array is in decreasing order, no next permutation will be found, hence return the array in sorted order.
Implementation of the Approach:
C++ Code
void nextPermutation(vector < int > & nums) {
int n = nums.size(), k, l;
for (k = n - 2; k >= 0; k--) {
if (nums[k] < nums[k + 1]) {
break;
}
}
if (k < 0) {
reverse(nums.begin(), nums.end());
} else {
for (l = n - 1; l > k; l--) {
if (nums[l] > nums[k]) {
break;
}
}
swap(nums[k], nums[l]);
reverse(nums.begin() + k + 1, nums.end());
}
}
Java Code
public void nextPermutation(int[] A) {
if (A == null || A.length <= 1) return;
int i = A.length - 2;
while (i >= 0 && A[i] >= A[i + 1]) i--;
if (i >= 0) {
int j = A.length - 1;
while (A[j] <= A[i]) j--;
swap(A, i, j);
}
reverse(A, i + 1, A.length - 1);
}
public void swap(int[] A, int i, int j) {
int tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}
public void reverse(int[] A, int i, int j) {
while (i < j) swap(A, i++, j--);
}
Python Code
def nextPermutation(self, nums):
i = j = len(nums) - 1
while i > 0 and nums[i - 1] >= nums[i]:
i -= 1
if i == 0:
nums.reverse()
return
k = i - 1
while nums[j] <= nums[k]:
j -= 1
nums[k], nums[j] = nums[j], nums[k]
l, r = k + 1, len(nums) - 1
while l < r:
nums[l], nums[r] = nums[r], nums[l]
l += 1
r -= 1
Time Complexity: O(N), where N is the total size of the array
Space Complexity: O(1), as no extra space is used.
Practice Questions:
FAQ
- What if the input array is sorted in decreasing order?
If the array is sorted in decreasing order, simply sort it in ascending order, since no greater permutation would be possible for such an array.
- What is the approach to solve the Next Permutation problem?
The idea is to find the longest non-increasing suffix and swap it with the pivot element found. Pivot element is the index where A[i] < A[i + 1]. At last reversing the suffix, gives us the next greater permutation.
