Permutation Of String

Problem Statement

Given a string S. The task is to print all the possible permutations of the given string.A permutation of a string S iis another string that contains the same characters, only the order of characters can be different.
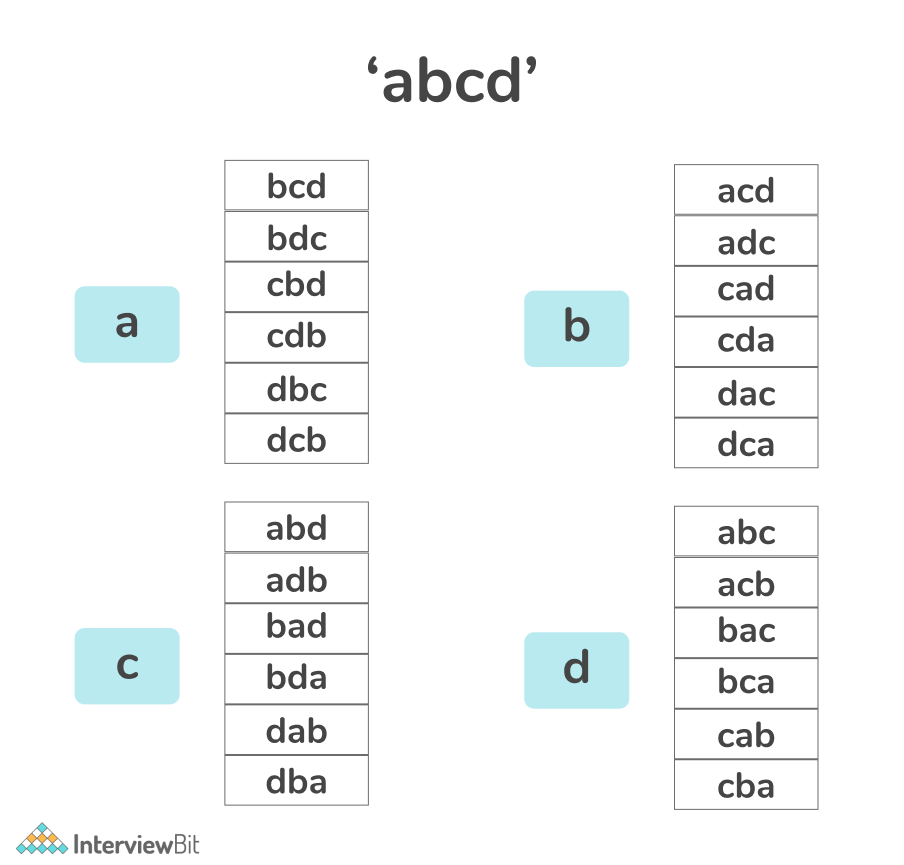
For example, “abcd” and “dabc” are permutations of each other.

Examples:
Input: S = “abc”
Output: [“abc”, “acb”, “bac”, “bca”, “cba”, “cab”]
Explanation:
All the permutations of the given string are given.

Approach: Backtracking

Using a backtracking approach, all the permutations of the given string can be printed.
Backtracking is an algorithm for finding all the possible solutions by exploring all possible ways.

If one of the found solutions turns out to not satisfy the given criteria, it discards the solution and makes some changes and backtracks again.

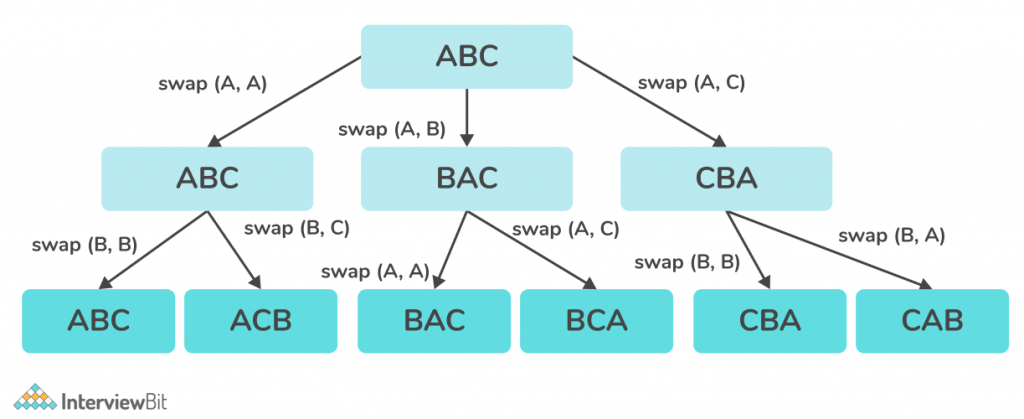
Algorithm:

• The backtracking function considers the first index of the given string.
• If the index is N, i.e. length of the string, it means that the current permutation is completed.
• Run a loop from current index idx till N – 1 and do the following:
  • Swap S[i] and S[idx].
  • Construct all other possible permutations, from backtrack(idx + 1).
  • Backtrack again, i.e. swap(S[i], S[idx]).

C++Implementation For Backtracking Method

void backtrack(string s, int idx, int N) {
    if (idx == N)
      cout << s << endl;
    else {
      for (int i = idx; i <= N; i++) {
        swap(s[idx], a[i]);
        permute(s, idx + 1, N);
        swap(s[idx], a[i]);
      }
    }
    solve() {
      string s = ”ABC”;
      int N = s.length();
      backtrack(s, 0, N - 1);
    }

JavaImplementation For Backtracking Method

 public String swap(String a, int i, int j) {
  char temp;
  char[] charArray = a.toCharArray();
  temp = charArray[i];
  charArray[i] = charArray[j];
  charArray[j] = temp;
  return String.valueOf(charArray);
}
private void backtrack(String s, int idx, int N) {
  if (idx == N)
    System.out.println(s);
  else {
    for (int i = idx; i <= N; i++) {
      s = swap(s, idx, i);
      backtrack(s, idx + 1, N);
      s = swap(s, idx, i);
    }
  }
}
solve() {
  String s = ”ABC”;
  int N = s.length;
  backtrack(s, 0, N - 1);
}

PythonImplementation For Backtracking Method

def toString(List):
    return ''.join(List)
 
def backtrack(s, idx, N):
    if idx == N:
        print(toString(s))
    else:
        for i in xrange(idx, N + 1):
            s[idx], s[i] = s[i], s[idx]
            backtrack(s, idx + 1, N)
            s[idx], s[i] = s[i], s[idx]
 
 
def solve():
    a = "ABC"
    N = len(s)
    s = list(a)
    permute(s, 0, N - 1)

Time Complexity: O(N * N!), where N is the length of the string.
Space Complexity: O(N!), since one has to keep N! solutions.

Practice Question

• Longest Substring Without Repeat

FAQs

Q.1: How to print a unique permutation of a string?

Ans: To print the unique permutations of the string, put the strings in a HashSet, hence it will give all unique permutations of the strings.

Q.2: What is the approach used to find permutations of a string?

Ans: The backtracking algorithm is to solve this problem.