Problem Statement
Given an array a[], find the number of subarrays in it, which have a sum of k.
Subarray: A subarray of an array is formed by deleting some(possibly zero) elements from the beginning or end of the array.
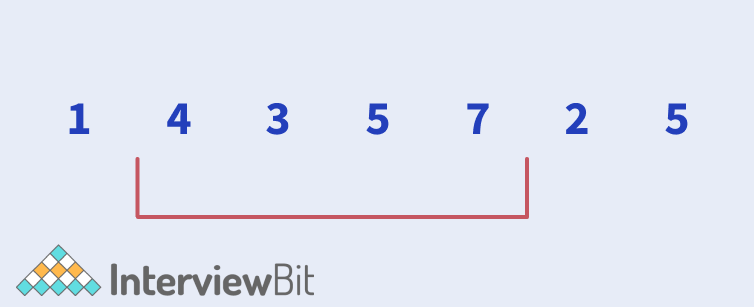
The red region shows a subarray of the original array.
Confused about your next job?
Sample Test Cases
Input 1: a = [10, 2, -2, -20, 10], k = -10
Output 1: 3
Explanation 1: The subarrays are listed as below (1 – Based Indexing):
- [4, 5]
- [1, 4]
- [2, 5]
Input 2: a = [1, 1, 1], k = 2
Output 2: 2
Explanation 2: All subarrays of length 2 are valid subarrays in this case, and there are a total of 2 such subarrays.
Naive Approach
The naive approach is to generate all the subarrays of the array and calculate their sum. Whenever we find a subarray with a sum equal to k, we increment our counter by 1. Finally, we return the count which keeps track of the number of subarrays with a sum equal to k.
Since there are a total of (n * (n + 1)) / 2 subarrays of an array, and each subarray will take O(n) time to traverse and calculate their sum, the required time complexity of this approach will be cubic in nature.
C++ Code
int countSubarraysWithSumK(vector < int > & a, int K) {
int n = a.size();
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int sum = 0;
for (int k = i; k <= j; k++) {
sum += a[k];
}
count += (sum == K);
}
}
return count;
}Java Code
public static int countSubarraysWithSumK(int[] a, int K) {
int n = a.length;
int count = 0;
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int sum = 0;
for (int k = i; k <= j; k++) {
sum += a[k];
}
count += (sum == K ? 1 : 0);
}
}
return count;
}Python Code
def countSubarrayswithSumK(a, K):
n = len(a)
count = 0
for i in range(n):
for j in range(i, n):
sum = 0
for k in range(i, j + 1):
sum += a[k]
count += sum == K
return countComplexity Analysis
- Time Complexity: O(n3)
- Space Complexity: O(1)
Optimal Approach
We can solve this problem in linear time complexity using a hashmap-based approach. The algorithm is described as follows:
- Traverse the array, and keep track of the current running sum up to the ith index in a variable, say sum.
- Also, hash the different values of the sum obtained so far, into a hashmap.
- If the sum equals k at any point in the array, increment the count of subarrays by 1.
- If this value of sum has exceeded k by a value of sum – k, we can find the number of subarrays, found so far with sum = sum – k, from our hashmap. Observe that if these subarrays are deleted from our current array, we will again obtain a sum of k. So, we add to our answer, the number of subarrays with sum = sum – k found so far from our hashmap.
- After traversing through the entire array once and applying the above steps, return the calculated result.

C++ Implementation
int countSubarraysWithSumK(vector < int > & a, int K) {
int n = a.size();
unordered_map < int, int > hash;
int count = 0, sum = 0;
for (int i = 0; i < n; i++) {
sum += a[i];
if (sum == K) {
count++;
}
if (hash.find(sum - K) != hash.end()) {
count += hash[sum - K];
}
hash[sum]++;
}
return count;
}Java Implementation
public static int countSubarraysWithSumK(int[] a, int K) {
int n = a.length;
HashMap < Integer, Integer > hash = new HashMap < > ();
int count = 0, sum = 0;
for (int i = 0; i < n; i++) {
sum += a[i];
if (sum == K) {
count++;
}
if (hash.get(sum - K) != null) {
count += hash.get(sum - K);
}
if (hash.get(sum) != null) {
hash.put(sum, hash.get(sum) + 1);
} else {
hash.put(sum, 1);
}
}
return count;
}Python Implementation
from collections import defaultdict
def countSubarrayswithSumK(a, K):
n = len(a)
hash = defaultdict(lambda: 0)
count = 0
sum = 0
for i in range(n):
sum += a[i]
if sum == K:
count += 1
if (sum - K) in hash:
count += hash[sum - K]
hash[sum] += 1
return countComplexity Analysis
- Time Complexity: O(n)
- Space Complexity: O(1)
Practice Problem
FAQs
Q. What is the time complexity of lookup in a hashmap?
A. The time complexity of lookup in a hashmap is O(1) amortized.
Q. Why is the number of subarrays of an array given by (n * (n + 1)) / 2?
A. The number of subarrays of an array can be calculated as there are,
- 1 subarray of length n
- 2 subarrays of length n – 1
- ……
- n subarrays of length 1
So, the total number of subarrays count out to a total of 1 + 2 + 3 + … n = (n * (n + 1)) / 2.







 Join WhatsApp Group
Join WhatsApp Group


