Subset Sum Problem

Problem Statement

Given an array of non-negative integers and an integer sum. We have to tell whether there exists any subset in an array whose sum is equal to the given integer sum.

Examples:

Input: arr[] = {3, 34, 4, 12, 3, 2}, sum = 7
Output: True
Explanation: There is a subset (4, 3) with sum 7.

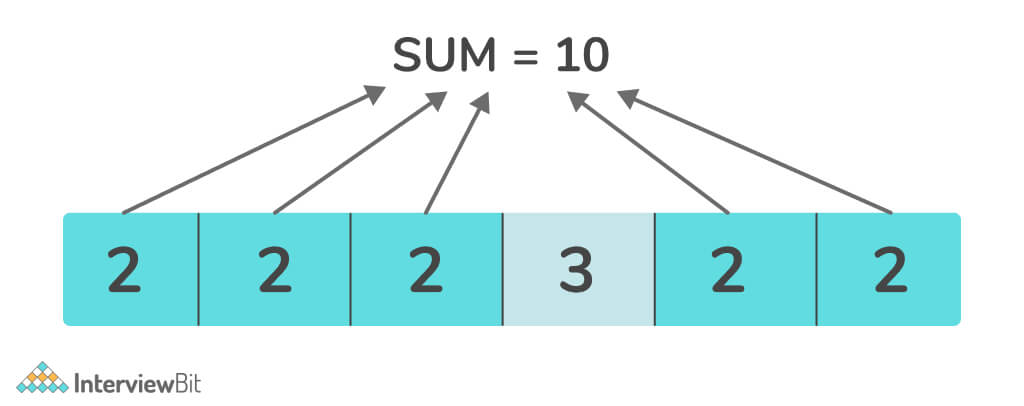
Input: arr[] = {2, 2, 2, 3, 2, 2}, sum = 10
Output: True
Explanation:

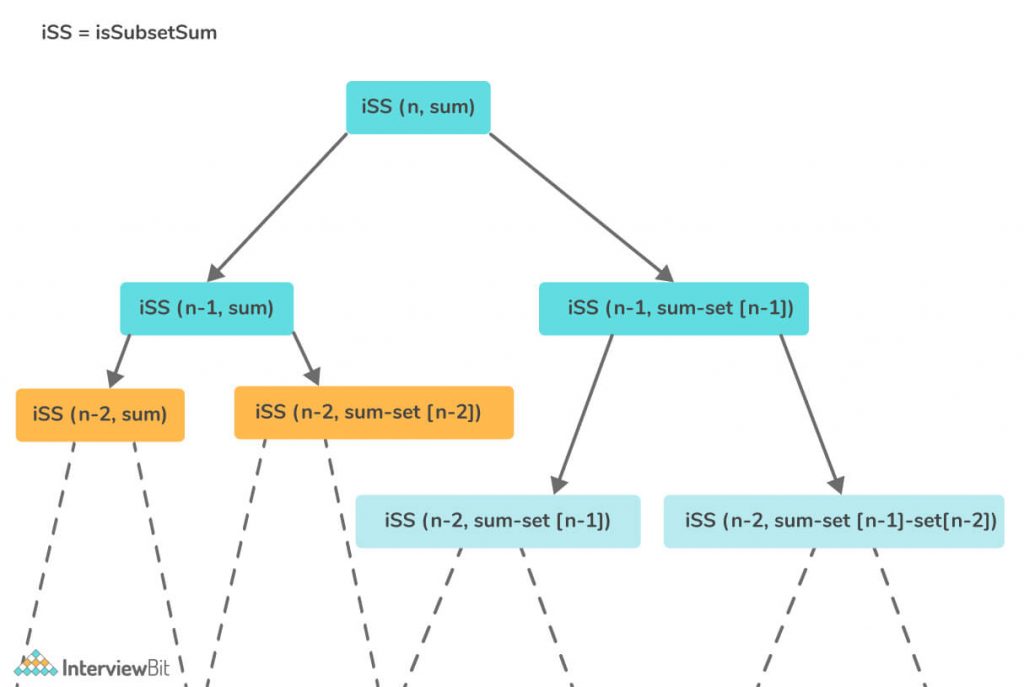
Recursive Approach

For this approach, we have two cases. 

• Let’s take the last element and now the sum = target sum – value of ‘last’ element and elements remaining = size of array – 1.
• Now  don’t take the ‘last’ element and now the  sum = target sum and elements remaining = size of array – 1.

Dry Run of the Approach:

Suppose n is the size of the array.

Base Cases

isThereSubsetSum(arr, n, sum) = false, if sum > 0 and n == 0
isThereSubsetSum(arr, n, sum) = true, if sum == 0

C Implementation Of Recursive Approach

bool isThereSubsetSum(int arr[], int n, int sum) {
  if (sum == 0)
    return true;
  if (n == 0)
    return false;

  if (arr[n - 1] > sum)
    return isThereSubsetSum(arr, n - 1, sum);

  return isThereSubsetSum(arr, n - 1, sum) ||
    isThereSubsetSum(arr, n - 1, sum - arr[n - 1]);
}

Java Implementation Of Recursive Approach

static boolean isThereSubsetSum(int arr[],
  int n, int sum) {

  if (sum == 0)
    return true;
  if (n == 0)
    return false;

  if (arr[n - 1] > sum)
    return isThereSubsetSum(arr, n - 1, sum);

  return isThereSubsetSum(arr, n - 1, sum) ||
    isThereSubsetSum(arr, n - 1, sum - arr[n - 1]);
}

Python Implementation Of Recursive Approach

def isThereSubsetSum(arr, n, sum):
    if (sum == 0):
        return True
    if (n == 0):
        return False
 
    if (arr[n - 1] > sum):
        return isThereSubsetSum(arr, n - 1, sum)
 
    return isThereSubsetSum(
        arr, n-1, sum) or isThereSubsetSum(
        arr, n-1, sum-arr[n-1])

Time complexity: The above approach may try all the possible subsets of a given array in the worst case. Therefore the time complexity of the above approach is exponential.

Dynamic Programming Approach

In this approach, we will make a 2D array of size equal to (size of array + 1) * (target sum + 1) of boolean type. The state dp[i][j] will be true if there is a subset of elements from A[0….i] with a sum value equal to j.

Approach:

• We make a boolean dp[][] and fill it in a top-down manner.
• The value of dp[i][j] will be true if there exists a subset of dp[0..i] with a sum equal to j., otherwise false
• Finally, we return dp[n][sum]

C Implementation For Subset Sum

bool isThereSubsetSum(int arr[], int n, int sum) {

  bool dp[n + 1][sum + 1];
  for (int i = 0; i <= n; i++)
    dp[i][0] = true;

  for (int i = 1; i <= sum; i++)
    dp[0][i] = false;
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= sum; j++) {
      if (j < arr[i - 1])
        dp[i][j] = dp[i - 1][j];
      if (j >= arr[i - 1])
        dp[i][j] = dp[i - 1][j] ||
        dp[i - 1][j - arr[i - 1]];
    }
  }
  return dp[n][sum];
}

Java Implementation For Subset Sum

static boolean isThereSubsetSum(int arr[], int n, int sum) {
  boolean dp[][] = new boolean[n + 1][sum + 1];
  for (int i = 0; i <= n; i++)
    dp[i][0] = true;

  for (int i = 1; i <= sum; i++)
    dp[0][i] = false;

  for (int i = 1; i <= sum; i++) {
    for (int j = 1; j <= n; j++) {
      if (j < arr[i - 1])
        dp[i][j] = dp[i - 1][j];
      if (j >= arr[i - 1])
        dp[i][j] = dp[i - 1][j] ||
        dp[i - 1][j - arr[i - 1]];
    }
  }
  return dp[n][sum];
}

Python Implementation For Subset Sum

def isThereSubsetSum(arr, n, sum):
     
    dp =([[False for i in range(sum + 1)]
            for i in range(n + 1)])
     
    for i in range(n + 1):
        dp[i][0] = True
         
    for i in range(1, sum + 1):
         dp[0][i]= False
             
   
    for i in range(1, n + 1):
        for j in range(1, sum + 1):
            if j<arr[i-1]:
                dp[i][j] = dp[i-1][j]
            if j>= arr[i-1]:
                dp[i][j] = (dp[i-1][j] or
                                dp[i - 1][j-arr[i-1]])
     
    return dp[n][sum]

Time Complexity: O(N * sum) where N is the size of the array.
Space Complexity: O(N * sum) where N is the size of the array.

Practice Questions

Minimum Difference Subsets
Subset Sum Problem
Equal Average Partition
Dynamic Programming

Frequently Asked Questions

What subset sum problem gives a suitable example?
The Subset-Sum Problem is to find a subset’ of the given array A = (A1 A2 A3…An) where the elements of the array A are n positive integers in such a way that a’∈A and summation of the elements of that subsets is equal to some positive integer S.

Is the subset sum problem NP-hard?
Yes, it is an NP-hard problem.

Is subset-sum an optimization problem?
Yes, subset-sum is an optimization problem because it has a variety of algorithms for tackling it.

How do you solve subsets?
Subsets can be solved using backtracking and dynamic programming with efficient time complexity.