Tower of Hanoi

What is the Tower of Hanoi?

The Tower of Hanoi is a mathematical puzzle. It consists of three rods and N disks. The task is to move all disks to another rod following certain rules:

1. Only one disk can be moved at a time.
2. Only the uppermost disk can be moved from one stack to the top of another stack or to an empty rod.
3. Larger disks cannot be placed on top of smaller disks.

Problem Statement: Program for Tower of Hanoi Algorithm

A diagrammatic illustration of the Tower of Hanoi:

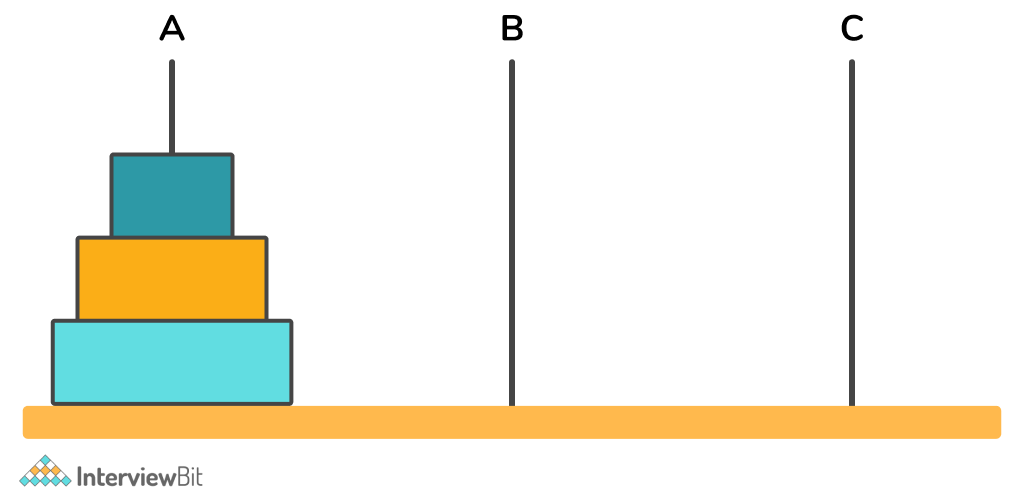
Image Source – Google images

The result is :

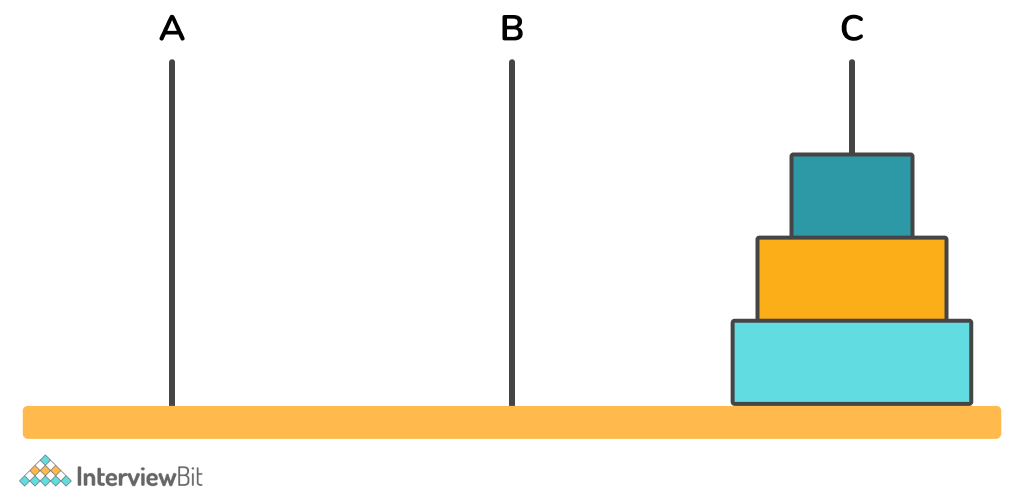
Image Source – Google Images.

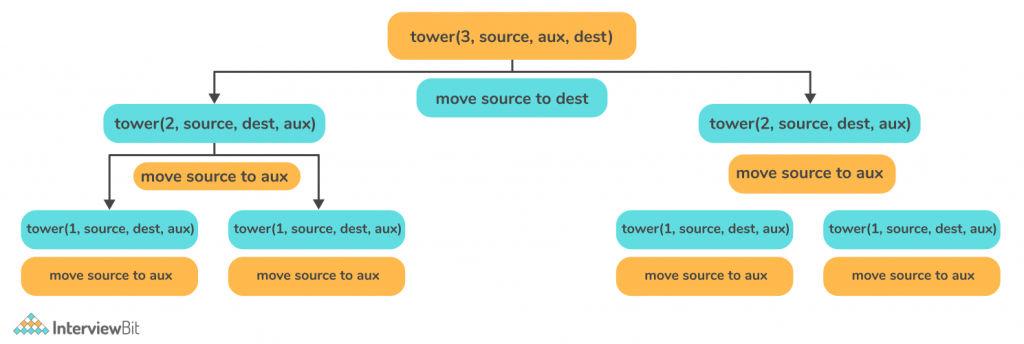
Recursive Approach

The idea is to use a recursive approach to solve this problem.
Let us try to solve the problem for N = 2.

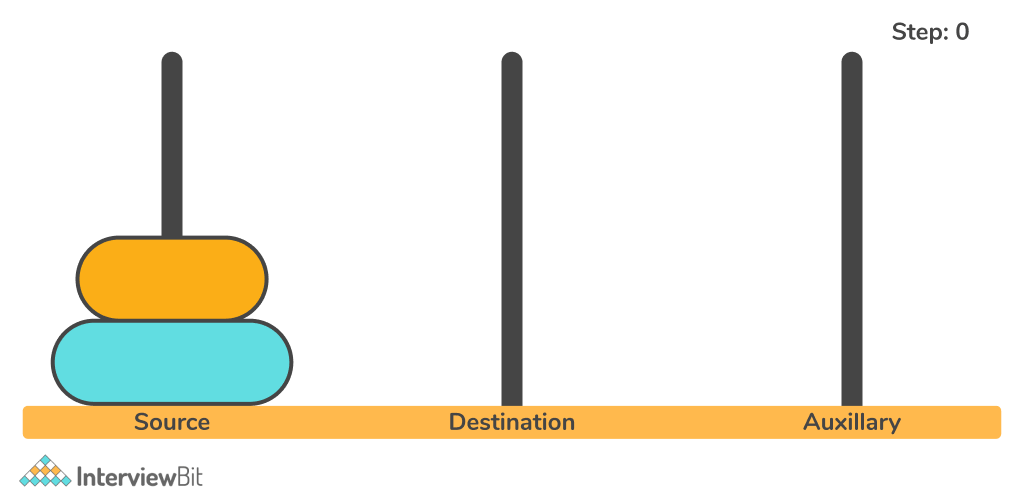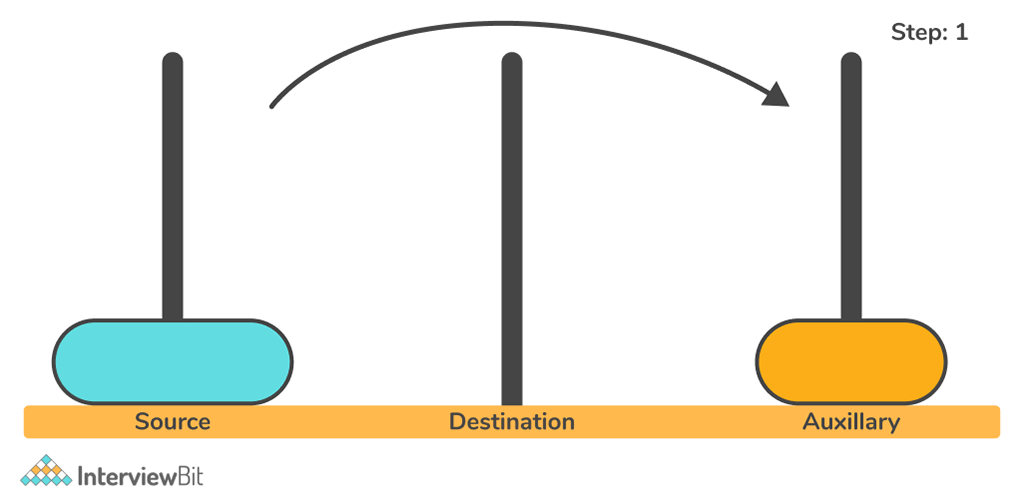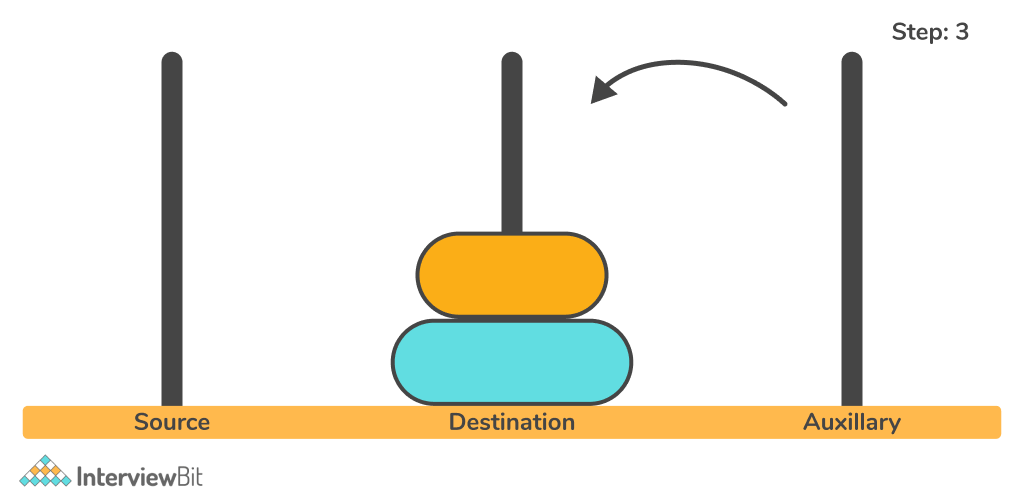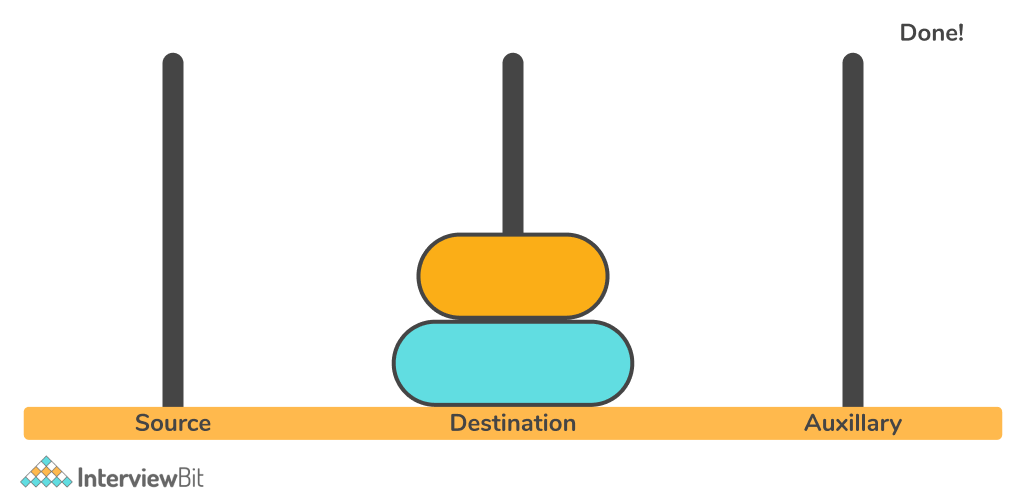
So, one disk is moved from rod 1 to rod 3. Then the second disk is moved from rod 1 to rod 2 and finally, the first disk is moved again back to rod 2.

Similarly, the problem can be solved recursively for N = 3. Observe the below example.

The minimum number of moves to solve the Tower of Hanoi problem is 2^N – 1, where N is the number of disks.

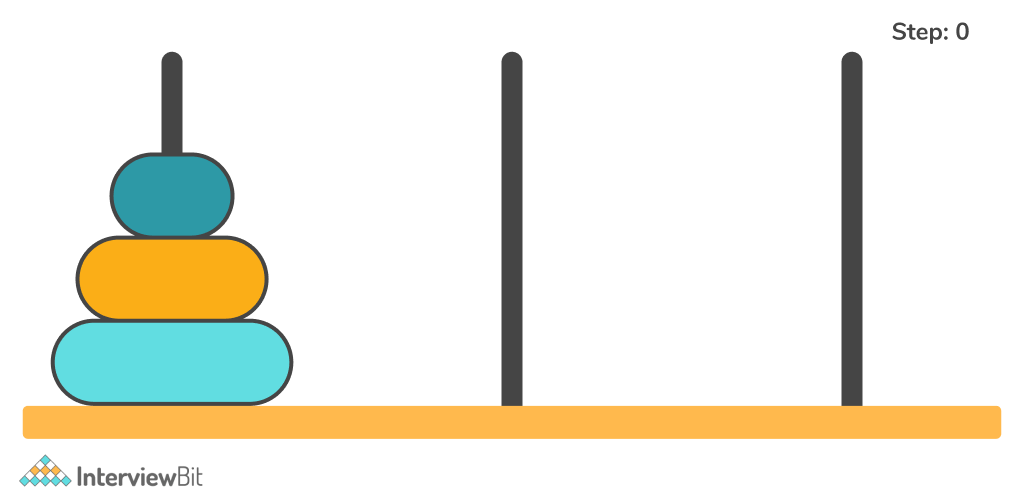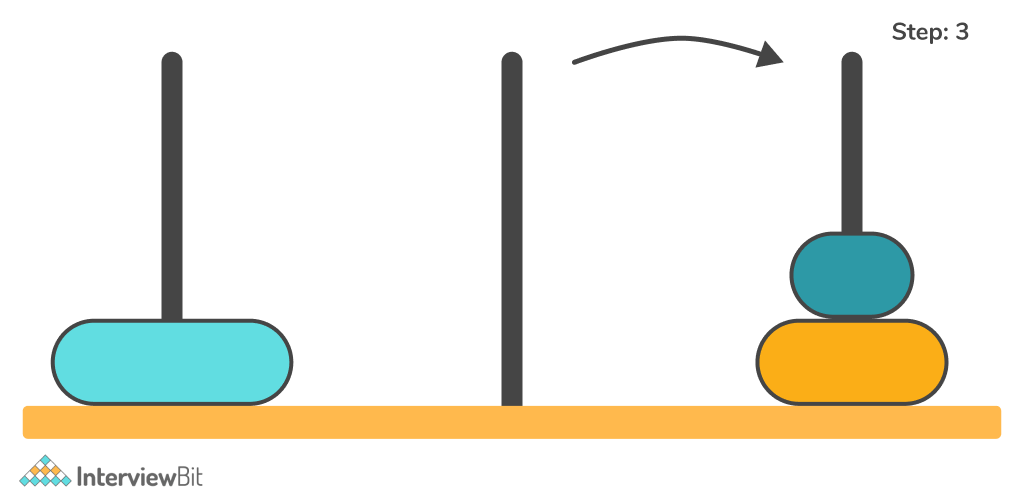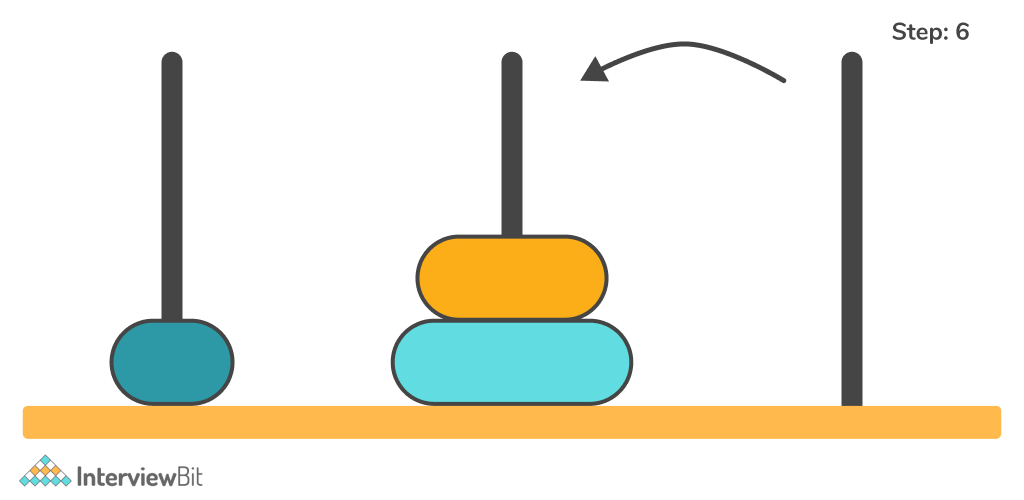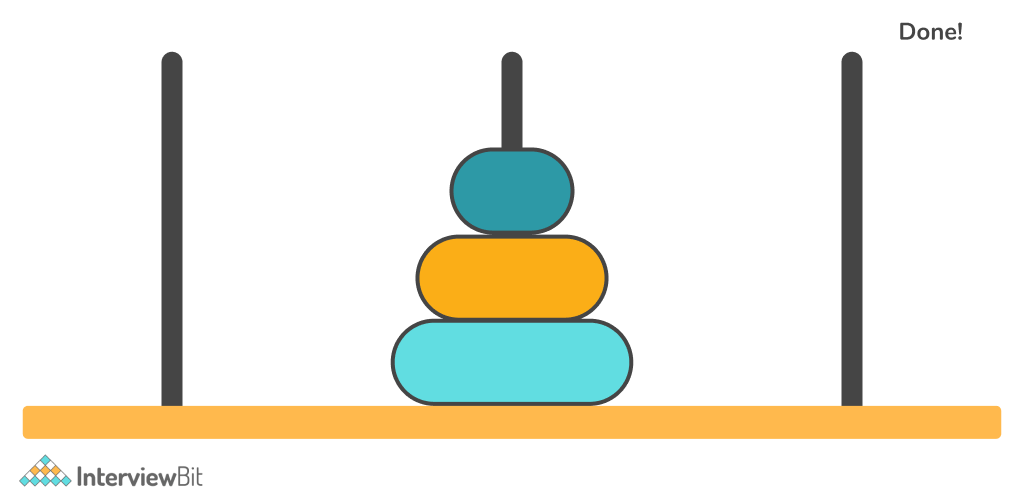
Dry Run of the above illustration –

• Move disc 1 from tower A to tower B.
• Move disc 2 from tower A to tower C. 
• Move disc 1 from tower B to tower C.
• Move Disc 3 from tower A to tower B.
• Move Disc 1 from tower C to tower A.
• Move Disc 2 from tower C to tower B.
• Move Disc 1 from tower A to tower B.

Algorithm

• Let us consider a recursive function that takes the following argument N, the number of disks, to_Rod, which indicates the rod which is moved to, from_rod, denoting the rod from which rod is removed, and aux_rod, denoting the rod which is used for transferring rods from from_rod to to_rod.
• The base case is for N = 1. Move it from source to destination, i.e. from_rod to to_rod.
• Solve the problem recursively by moving disk 1, 2, 3,…, N – 1 i.e. from_rod to aux_rod  by recursively calling the function on (N – 1, from_rod, aux_rod, to_rod).
• Now, since the top N – 1 disks have been removed from from_rod, move the last disk from from_rod to to_rod.
• Similarly, again remove the top N – 1 disk from aux_rod to to_rod and recursively call the function on (N – 1, aux_rod, to_rod, from_rod)
• Repeat the above steps until it reaches the base case.

C++ Code for Recursive Approach

void towerOfHanoi(int n, char from_rod, char to_rod, char aux_rod)
{
    if (n == 1)
    {
        cout << "Move disk 1 from rod " << from_rod <<
                            " to rod " << to_rod<<endl;
        return;
    }
    towerOfHanoi(n - 1, from_rod, aux_rod, to_rod);
    cout << "Move disk " << n << " from rod " << from_rod <<
                                " to rod " << to_rod << endl;
    towerOfHanoi(n - 1, aux_rod, to_rod, from_rod);
}
solve(){
      TowerOfHanoi(n, 'A', 'C', 'B');
}

Java Code for Recursive Approach

static void towerOfHanoi(int n, char from_rod, char to_rod, char aux_rod)
{
    if (n == 1)
    {
        System.out.println("Move disk 1 from rod "+
                           from_rod+" to rod "+to_rod);
        return;
    }
    towerOfHanoi(n - 1, from_rod, aux_rod, to_rod);
    System.out.println("Move disk "+ n + " from rod " +
                       from_rod +" to rod " + to_rod );
    towerOfHanoi(n - 1, aux_rod, to_rod, from_rod);
}
 
solve(){
   TowerOfHanoi(n, 'A', 'C', 'B')
 
}

Python Code for Recursive Approach

def TowerOfHanoi(n , from_rod, to_rod, aux_rod):
    if n == 1:
        print("Move disk 1 from rod",from_rod,"to rod",to_rod)
        return
    TowerOfHanoi(n-1, from_rod, aux_rod, to_rod)
    print("Move disk",n,"from rod",from_rod,"to rod",to_rod)
    TowerOfHanoi(n-1, aux_rod, to_rod, from_rod)
 
def solve():
      TowerOfHanoi(n, 'A', 'C', 'B');

Time Complexity: O(2^N) where N is the number of disks.
Space Complexity: O(N), as the disks, take up the recursive stack space.

Frequently Asked Questions

Q.1: What are the minimum moves to solve the Tower of Hanoi problem?

Ans: The minimum moves required is 2^N – 1 to move all disks from Source rod A to destination rod B while following the rules.

Q.2: What is the space complexity of the Tower of Hanoi?

Ans: The space complexity is O(N) since, for each recursion, the disks take up N – 1 recursive stack space.