26K
0
9 minute read

Vertical Order Traversal Of Binary Tree

November 19, 2021
​​Vertical Order Traversal of Binary Tree
Table Of Contents
show

Problem Statement

Given a binary tree, print it vertically.

Sample Test Cases

Input 1:

Confused about your next job?

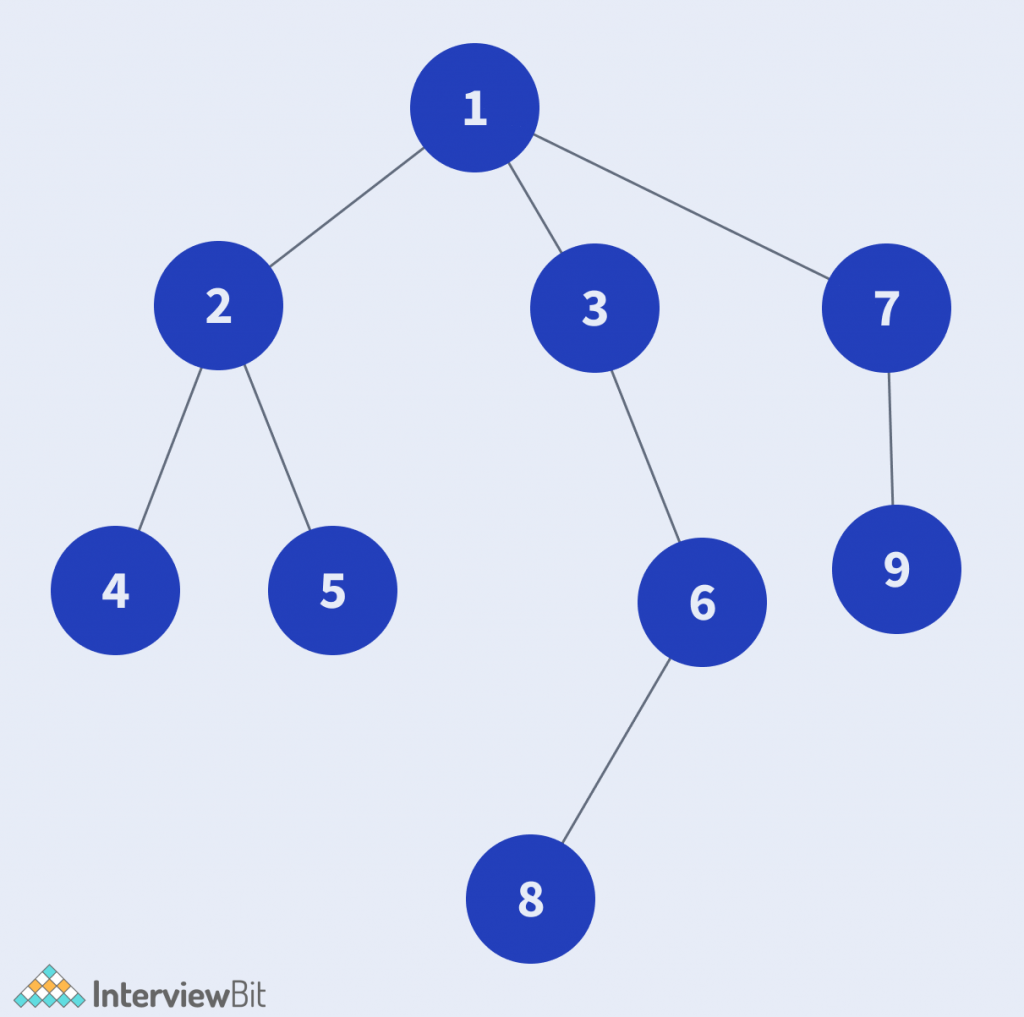
In 4 simple steps you can find your personalised career roadmap in Software development for FREE



Expand in New Tab 

Output 1:

4
2
1 5 6
3 8
7 
9

Explanation 1:

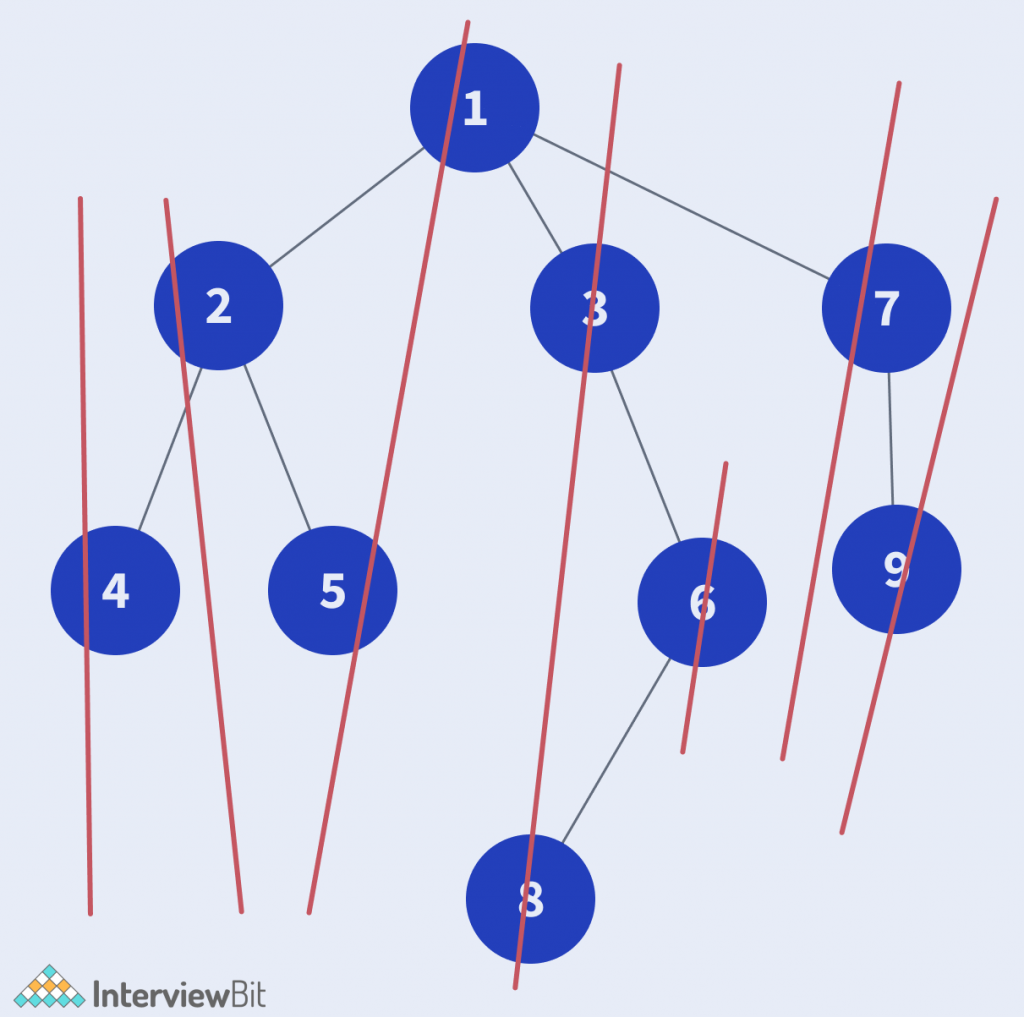
The diagram shows how the vertical traversal of the tree is calculated.

Naive Approach

The naive idea is to find the maximum and minimum horizontal distances with respect to the root of the graph. After we have the range [min, max], we iterate over all the lines from the minimum to the maximum(refer to diagram above) and print the nodes lying on those lines in order. The traversal on the tree can be done recursively as follows for the horizontal distances.

  • function(root.left, distance – 1)
  • function(root.right, distance + 1)

At each step of recursion, we take the maximum and minimum of the distance.

C++ Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
  public:
    void distanceRoot(TreeNode * root, int & low, int & high, int horDist) {
      if (root == NULL) {
        return;
      }
      low = min(low, horDist);
      high = max(high, horDist);
      distanceRoot(root -> left, low, high, horDist - 1);
      distanceRoot(root -> right, low, high, horDist + 1);
    }
  void getFromLine(TreeNode * root, int num, int horDist, vector < int > & line) {
    if (root == NULL) {
      return;
    }
    if (horDist == num) {
      line.push_back(root -> val);
    }
 getFromLine(root -> left, num, horDist - 1, line);
    getFromLine(root -> right, num, horDist + 1, line);
  }
  vector < vector < int >> verticalTraversal(TreeNode * root) {
    vector < vector < int >> result;
    int low = 0, high = 0;
    distanceRoot(root, low, high, 0);
    for (int i = low; i <= high; i++) {
      vector < int > line;
      getFromLine(root, i, 0, line);
      result.push_back(line);
    }
    return result;
  }
};

Java Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
  public void distanceRoot(TreeNode root, int[] low, int[] high, int horDist) {
    if (root == null) {
      return;
    }
    low[0] = Math.min(low[0], horDist);
    high[0] = Math.max(high[0], horDist);
    distanceRoot(root.left, low, high, horDist - 1);
    distanceRoot(root.right, low, high, horDist + 1);
  }
  public void getFromLine(TreeNode root, int num, int horDist, List < Integer > line[]) {
    if (root == null) {
      return;
    }
    if (horDist == num) {
      line[0].add(root.val);
    }
    getFromLine(root.left, num, horDist - 1, line);
    getFromLine(root.right, num, horDist + 1, line);
  }
  public List < List < Integer >> verticalTraversal(TreeNode root) {
    List < List < Integer >> result = new ArrayList < > ();
    int[] low = new int[1];
    int[] high = new int[1];
    distanceRoot(root, low, high, 0);
    for (int i = low[0]; i <= high[0]; i++) {
      List < Integer > line[] = new ArrayList[1];
      line[0] = new ArrayList < Integer > ();
      getFromLine(root, i, 0, line);
      result.add(line[0]);
    }
    return result;
  }
}

Python Code

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def distanceRoot(self, root, low, high, horDist):
        if not root:
            return
        low[0] = min(low[0], horDist)
        high[0] = max(high[0], horDist)
        self.distanceRoot(root.left, low, high, horDist - 1)
        self.distanceRoot(root.right, low, high, horDist + 1)
  def getFromLine(self, root, num, horDist, line):
        if not root:
            return
        if horDist == num:
            line.append(root.val)
        self.getFromLine(root.left, num, horDist - 1, line)
        self.getFromLine(root.right, num, horDist + 1, line)

    def verticalTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        low = [0]
        high = [0]
        result = []
        self.distanceRoot(root, low, high, 0)
        for i in range(low[0], high[0] + 1):
            line = []
            self.getFromLine(root, i, 0, line)
            result.append(line)
        return result

Complexity Analysis

  • Time Complexity: O(n * n)
  • Space Complexity: O(n)

Approach 2 (HashMap Based Approach)

We can optimize the above naive approach by using a hashmap. Observe that all nodes which have the same horizontal distance from the root, lie on the same vertical line. So, by making the horizontal distances the key of the map, we can recursively push the nodes, into the proper key container while calculating the horizontal distances in the same recursive calls themselves.

The algorithm is as follows:

  • Initialize a Map with [Key, Value] pair as [Integer, Vector<Integer>].
  • Recursively traverse on the tree (both left and right child) keeping track of the horizontal distances with respect to the root node.
  • With the current horizontal distance as the key, push the current node, into the map of vectors.
  • Once the recursion terminates, we store each of the values(vectors) in the map, for distinct keys, and return them.

The thing to note about this approach is that it may not print the nodes in the same vertical order in which they appear in the tree.

C++ Implementation

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
  public:
    void getVerticalTraversal(TreeNode * root, int horDist, map &lt; int, vector &lt; int &gt;&gt; &amp; m) {
      if (root == NULL) {
        return;
      }
      m[horDist].push_back(root -&gt; val);
      getVerticalTraversal(root -&gt; left, horDist - 1, m);
      getVerticalTraversal(root -&gt; right, horDist + 1, m);
    }
  vector &lt; vector &lt; int &gt;&gt; verticalTraversal(TreeNode * root) {
    map &lt; int, vector &lt; int &gt;&gt; m;
    getVerticalTraversal(root, 0, m);
    vector &lt; vector &lt; int &gt;&gt; result;
    for (auto x: m) {
      result.push_back(x.second);
   }
    return result;
  }
};

Java Implementation

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public void getFromLine(TreeNode root, int num, int horDist, List &lt; Integer &gt; line[]) {
    if (root == null) {
      return;
    }
    if (horDist == num) {
      line[0].add(root.val);
    }
    getFromLine(root.left, num, horDist - 1, line);
    getFromLine(root.right, num, horDist + 1, line);
  }
  public List &lt; List &lt; Integer &gt;&gt; verticalTraversal(TreeNode root) {
    List &lt; List &lt; Integer &gt;&gt; result = new ArrayList &lt; &gt; ();
    int[] low = new int[1];
    int[] high = new int[1];
    distanceRoot(root, low, high, 0);
 for (int i = low[0]; i &lt;= high[0]; i++) {
      List &lt; Integer &gt; line[] = new ArrayList[1];
      line[0] = new ArrayList &lt; Integer &gt; ();
      getFromLine(root, i, 0, line);
      result.add(line[0]);
    }
    return result;
  }
}

Python Implementation

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def getVerticalTraversal(self, root, horDist, m):
        if not root:
            return
        try:
            m[horDist].append(root.val)
        except:
            m[horDist] = [root.val]
        self.getVerticalTraversal(root.left, horDist - 1, m)
        self.getVerticalTraversal(root.right, horDist + 1, m)

    def verticalTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        result = []
        m = dict()
        self.getVerticalTraversal(root, 0, m)
        for res in sorted(m.keys()):
            result.append(m[res])
        return result

Complexity Analysis:

  • Time Complexity: O(n * logn) or O(n) depending on the type of map used.
  • Space Complexity: O(n)

Approach 3 (BFS Based Approach)

To solve the issue of the nodes not coming in order, we can use a level order traversal-based approach on this tree. Using level order traversal ensures that a node that is below another node in the same vertical line, comes after that node when the results are being printed. The algorithm is described as follows:

  • Declare a map for branches of each node.
  • Start a BFS or level order traversal from each node.
  • Initialize a queue, which holds the following information, the data of the node and its horizontal distance from the root (can also be identified as its line number).
  • Now while the queue is not emptied, do the following,
    • Take the top element from the queue, pop it, and add its data in the corresponding branch’s vector.
    • If the left child of the node is not null, push it into the queue, with branch number as current branch number – 1.
    • If the right child of the node is not null, push it into the queue, with branch number as current branch number + 1.
  • Print/Return the values from the map accordingly in proper order.

C++ Code For BFS Approach

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
  public:
    void getTraversal(TreeNode * root, vector &lt; vector &lt; int &gt;&gt; &amp; res) {
      if (root == NULL) {
        return;
  }
      int horDist = 0;
      map &lt; int, vector &lt; int &gt;&gt; m;
      queue &lt; pair &lt; TreeNode * , int &gt;&gt; q;
      q.push({
        root,
        horDist
      });
      while (!q.empty()) {
        auto x = q.front();
        q.pop();
        TreeNode * u = x.first;
        horDist = x.second;
        m[horDist].push_back(u -&gt; val);
        if (u -&gt; left != NULL) {
          q.push({
            u -&gt; left,
            horDist - 1
          });
        }
        if (u -&gt; right != NULL) {
          q.push({
            u -&gt; right,
            horDist + 1
          });
        }
      }
      for (auto x: m) {
        res.push_back(x.second);
      }
    }
  vector &lt; vector &lt; int &gt;&gt; verticalTraversal(TreeNode * root) {
    vector &lt; vector &lt; int &gt;&gt; result;
    getTraversal(root, result);
    return result;
  }
};

Java Code For BFS Approach 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Q_pair {
  int hor_dist;
  TreeNode node;
  Q_pair(int hor_dist, TreeNode node) {
    this.hor_dist = hor_dist;
    this.node = node;

  }
}
class Solution {
  public List &lt; List &lt; Integer &gt;&gt; verticalTraversal(TreeNode root) {
    List &lt; List &lt; Integer &gt;&gt; result = new ArrayList &lt; &gt; ();
    if (root == null)
      return result;
    TreeMap &lt; Integer, List &lt; Integer &gt; &gt; map = new TreeMap &lt; &gt; ();
    int hor_d = 0;
    Queue &lt; Q_pair &gt; q = new LinkedList &lt; &gt; ();
    q.add(new Q_pair(0, root));
    while (!q.isEmpty()) {
      Q_pair temp = q.poll();
      hor_d = temp.hor_dist;
      TreeNode node = temp.node;
   if (map.containsKey(hor_d)) {
        map.get(hor_d).add(node.val);
      } else {
        List &lt; Integer &gt; arr = new ArrayList &lt; &gt; ();
        arr.add(node.val);
        map.put(hor_d, arr);
      }
      if (node.left != null)
        q.add(new Q_pair(hor_d - 1, node.left));
      if (node.right != null)
        q.add(new Q_pair(hor_d + 1, node.right));
    }

    for (Map.Entry &lt; Integer, List &lt; Integer &gt; &gt; entry: map.entrySet()) {
      result.add(entry.getValue());

    }
    return result;
  }
}

Python Code For BFS Approach 

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def traverse(self, root, res):
        if not root:
            return
        queue = []
        m = {}
        horDistm = {}
        queue.append(root)
        horDistm[root] = 0
        m[0] = [root.val]
        while len(queue) &gt; 0:
            u = queue.pop(0)
            if u.left:
                queue.append(u.left)
                horDistm[u.left] = horDistm[u] - 1
                horDist = horDistm[u.left]
                if m.get(horDist) is None:
                    m[horDist] = []
                    m[horDist].append(u.left.val)
                else:
                    m[horDist].append(u.left.val)
            if u.right:
                queue.append(u.right)
                horDistm[u.right] = horDistm[u] + 1
                horDist = horDistm[u.right]
                if m.get(horDist) is None:
                    m[horDist] = []
 m[horDist].append(u.right.val)
                else:
                    m[horDist].append(u.right.val)
        m_ = collections.OrderedDict(sorted(m.items()))
        for i in m_.values():
            res.append(i)

    def verticalTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[List[int]]
        """
        res = []
        self.traverse(root, res)
        return res

Complexity Analysis:

  • Time Complexity: O(n * logn) or O(n) depending on the type of map used.
  • Space Complexity: O(n)

Practice Problem

Vertical Order Traversal

FAQs

Q. How does the type of map determine the time complexity of the programs?
A. Different maps are implemented internally in different manners. Some are implemented using hashing, taking up constant lookup times, while others are implemented using AVL or Red-Black Trees which take up a logarithmic factor for lookups and updates.

Q. What are the different ways of traversing a binary tree?
A. There are different ways of traversing a binary tree such as Preorder Traversal, Postorder Traversal, Level Order Traversal, etc.

0
0
0
0
Share 0
Tweet 0
Pin it 0
Share 0
Share
Share
Share
Tweet
Previous Post
Intersection of Two linked lists

Intersection of Two Linked Lists

June 8, 2022
Next Post
JavaScript Frameworks

7 Top JavaScript Frameworks You Must Know in 2023

April 20, 2023
Total
0
Share
0
0
0
0
0