Insertion sort is the sorting mechanism where the sorted array is built having one item at a time. The array elements are compared with each other sequentially and then arranged simultaneously in some particular order. The analogy can be understood from the style we arrange a deck of cards. This sort works on the principle of inserting an element at a particular position, hence the name Insertion Sort.

Quick Navigation

1. Working
2. Pseudocode
3. Example program in C, C++, Java & Python
4. Time Complexity

Insertion Sort works as follows:

1. The first step involves the comparison of the element in question with its adjacent element.
2. And if at every comparison reveals that the element in question can be inserted at a particular position, then space is created for it by shifting the other elements one position to the right and inserting the element at the suitable position.
3. The above procedure is repeated until all the element in the array is at their apt position.

Let us now understand working with the following example:

Consider the following array: 25, 17, 31, 13, 2

First Iteration: Compare 25 with 17. The comparison shows 17< 25. Hence swap 17 and 25.

The array now looks like:

17, 25, 31, 13, 2

First Iteration

Second Iteration: Begin with the second element (25), but it was already swapped on for the correct position, so we move ahead to the next element.

Now hold on to the third element (31) and compare with the ones preceding it.

Since 31> 25, no swapping takes place.

Also, 31> 17, no swapping takes place and 31 remains at its position.

The array after the Second iteration looks like:

17, 25, 31, 13, 2

Second Iteration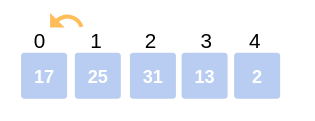

Third Iteration: Start the following Iteration with the fourth element (13), and compare it with its preceding elements.

Since 13< 31, we swap the two.

Array now becomes: 17, 25, 13, 31, 2.

But there still exist elements that we haven’t yet compared with 13. Now the comparison takes place between 25 and 13. Since, 13 < 25, we swap the two.

The array becomes 17, 13, 25, 31, 2.

The last comparison for the iteration is now between 17 and 13. Since 13 < 17, we swap the two.

The array now becomes 13, 17, 25, 31, 2.

Third Iteration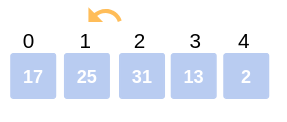

Fourth Iteration: The last iteration calls for the comparison of the last element (2), with all the preceding elements and make the appropriate swapping between elements.

Since, 2< 31. Swap 2 and 31.

Array now becomes: 13, 17, 25, 2, 31.

Compare 2 with 25, 17, 13.

Since, 2< 25. Swap 25 and 2.

13, 17, 2, 25, 31.

Compare 2 with 17 and 13.

Since, 2<17. Swap 2 and 17.

Array now becomes:

13, 2, 17, 25, 31.

The last comparison for the Iteration is to compare 2 with 13.

Since 2< 13. Swap 2 and 13.

The array now becomes:

2, 13, 17, 25, 31.

This is the final array after all the corresponding iterations and swapping of elements.

Fourth Iteration

Pseudocode

INSERTION-SORT(A)
   for i = 1 to n
   	key ← A [i]
    	j ← i – 1
  	 while j > = 0 and A[j] > key
   		A[j+1] ← A[j]
   		j ← j – 1
   	End while 
   	A[j+1] ← key
  End for 

Implementation:

Following are C, C++, Java and Python implementations of Insertion Sort.

Insertion sort Implementation in C:
#include <stdio.h>
#include <stdbool.h>

#define MAX 7	//defining size of our array

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
  int i;

  for(i = 0;i < count-1;i++) {
     printf("=");
  }

  printf("=\n");
}

void display() {
  int i;
  printf("[");

  // navigate through all items 
  for(i = 0;i < MAX;i++) {
     printf("%d ",intArray[i]);
  }

  printf("]\n");
}

void insertionSort() {

  int valueToInsert;
  int holePosition;
  int i;
 
  // loop through all numbers 
  for(i = 1; i < MAX; i++) { 

     // select a value to be inserted. 
     valueToInsert = intArray[i];

     // select the hole position where number is to be inserted 
     holePosition = i;

     // check if previous no. is larger than value to be inserted 
     while (holePosition > 0 && intArray[holePosition-1] > valueToInsert) {
        intArray[holePosition] = intArray[holePosition-1];
        holePosition--;
        printf(" item moved : %d\n" , intArray[holePosition]);
     }

     if(holePosition != i) {
        printf(" item inserted : %d, at position : %d\n" , valueToInsert,holePosition);
        // insert the number at current hole
        intArray[holePosition] = valueToInsert;
     }

     printf("Iteration %d#:",i);
     display();

  } 
}

void main() {
  printf("Input Array: ");
  display();
  printline(50);
  insertionSort();
  printf("Output Array: ");
  display();
  printline(50);
}

Insertion sort Implementation in C++:
#include <stdlib.h>
#include <iostream>

using namespace std;

//member functions declaration
void insertionSort(int arr[], int length);
void printArray(int array[], int size);

// main function
int main() 
{
    int array[6] = {5, 1, 6, 2, 4, 3};
    // calling insertion sort function to sort the array
    insertionSort(array, 6);
    return 0;
}

void insertionSort(int arr[], int length) 
{
    int i, j, key;
    for (i = 1; i < length; i++) 
    {
        key = arr[i];
        j = i-1;
        
        while (j >= 0 && arr[j] >key) 
        {
            arr[j+1] = arr[j];
            j--;
        }
        arr[j +1] = key;
        
    }
    cout << "Sorted Array: ";
    // print the sorted array
    printArray(arr, length);
}

// function to print the given array 
void printArray(int array[], int size)
{ 
    int j;
    for (j = 0; j < size; j++)
    {
        cout <<" "<< array[j];  
    }
    cout << endl;
}

// Java program for implementation of Insertion Sort
public class InsertionSort
{
    /*Function to sort array using insertion sort*/
    void sort(int arr[])
    {
        int n = arr.length;
        for (int i=1; i<n; ++i)
        {
            int key = arr[i];
            int j = i-1;
            
            /* Move elements of arr[0..i-1], that are
            greater than key, to one position ahead
            of their current position */
            while (j>=0 && arr[j] > key)
            {
                arr[j+1] = arr[j];
                j = j-1;
            }
            arr[j+1] = key;
        }
    }
    /* A utility function to print array of size n*/
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
    // Driver method
    public static void main(String args[])
    {
        int arr[] = {12, 11, 13, 5, 6};
        InsertionSort ob = new InsertionSort();
        ob.sort(arr);
        printArray(arr);
    }
}

Insertion sort Implementation in Python:
# Function to do insertion sort
def insertionSort(arr):
    # Traverse through 1 to len(arr)
    for i in range(1, len(arr)):
        key = arr[i]
        # Move elements of arr[0..i-1], that are
        # greater than key, to one position ahead
        # of their current position
        j = i-1
        while j >=0 and key < arr[j] :
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = key 
# Driver code to test above
arr = [12, 11, 13, 5, 6]
insertionSort(arr)
print ("Sorted array is:")
for i in range(len(arr)):
    print arr[i]