How does Binary Search Work?

Binary search works by repeatedly dividing the array into two halves that can contain the given target element, till the search area is limited to just one element. The necessary condition for binary search to work is the array needs to be sorted

Binary Search Example:

Given a sorted array, find if element 2 is present in the array.

Step 1: The given array:

Step 2: Consider two pointers, low = 0 and high = N - 1, where N is the size of the array.

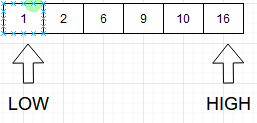
Step 3: Find the mid, i.e. mid = (low + high) / 2. Here, mid = (0 + 6) / 2 = 3.

 Step 4: Now, check for three conditions:

• Compare if A[mid] = 2
• Compare if A[mid] > 2
• Compare if A[mid] < 2
• It can be observed that, A[mid] = 9, which is > 2, therefore, we shift, high = mid - 1.

Step 5: If A[mid] < 2, shift low = mid + 1.

Step 6: Repeat Steps 3 to Step 5, until the search area is limited to just one element i.e. low = high.

Step 7: The value 2 is found.

Binary Search Implementations

Binary Search can be implemented in mainly two ways:

• Recursive method
• Iterative method

Let us first discuss the Recursive method.

Recursive Method

int bSearch(int arr[], int left, int right, int target) {
    if (right >= left) {
        int mid = left + (right - left) / 2;
 
        if (arr[mid] == target)
            return mid;
 
        if (arr[mid] > target)
            return binarySearch(arr, left, mid - 1, target);
 
        return binarySearch(arr, mid + 1, right, target);
    }
    return -1;
}

class BinarySearch {
    int bSearch(int arr[], int left, int right, int target) {
        if (right >= l) {
            int mid = l + (r - l) / 2;
 
            if (arr[mid] == target)
                return mid;
 
            if (arr[mid] > target)
                return binarySearch(arr, left, mid - 1, target);

            return binarySearch(arr, mid + 1, r, x);
       }
       return -1;
   }
}

def bSearch(arr, left, right, target):
    if right >= left:
 
        mid = left + (right - left) // 2

        if arr[mid] == target:
            return mid
 
        elif arr[mid] > target:
            return binarySearch(arr, left, mid-1, target)
 
        else:
            return binarySearch(arr, mid + 1, right, target)
 
    else:
        return -1

int bSearch(int arr[], int left, int right, int target) {
    while (left <= right) {
        int m = left + (right - left) / 2;
 
        if (arr[m] == target)
            return m;
 
        if (arr[m] < target)
            left = m + 1;
 
        else
            right = m - 1;
    }

    return -1;
}

class BinarySearch {
    int bSearch(int arr[], int left, int right, int target)
    {
        int left = 0, right = arr.length - 1;
        while (left <= right) {
            int m = left + (right - left) / 2;
 
            if (arr[m] == target)
                return m;
 
            if (arr[m] < target)
                left = m + 1;
 
            else
                right = m - 1;
        }
        return -1;
    }
}

def bSearch(arr, left, right, target):
    while left <= right:
 
        mid = left + (right - left) // 2
 
        if arr[mid] == target:
            return mid
 
        elif arr[mid] < target:
            left = mid + 1
 
        else:
            right = mid - 1
 
    return -1

Walkthrough Examples :

COUNTELEMENTS ROTATEDARRAY